题目内容
 如图所示,两带电平行板A、B间的电场为匀强电场,场强E=4.0×102V/m,两板相距d=0.16m,板长L=0.30m.一带电量q=1.0×10-16C、质量m=1.0×10-22㎏的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转,不计带电粒子所受重力,求:
如图所示,两带电平行板A、B间的电场为匀强电场,场强E=4.0×102V/m,两板相距d=0.16m,板长L=0.30m.一带电量q=1.0×10-16C、质量m=1.0×10-22㎏的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转,不计带电粒子所受重力,求:(1)粒子带何种电荷;
(2)要使粒子能飞出电场,粒子飞入电场时的速度v0至少为多大;
(3)粒子飞出电场时最大偏角的正切值tanθ.
分析:(1)平行金属板B板带负电,粒子向B板偏转,则粒子带正电.
(2)当粒子恰好从B板右侧边缘飞出电场时,此时粒子的速度为粒子飞出电场时最小速度.此时粒子水平位移为L,竖直位移为
,根据牛顿第二定律求出加速度,由运动学公式求出初速度.
(3)分解速度,求出偏转角的正切,再求粒子飞出电场时的最大偏角.
(2)当粒子恰好从B板右侧边缘飞出电场时,此时粒子的速度为粒子飞出电场时最小速度.此时粒子水平位移为L,竖直位移为
| d |
| 2 |
(3)分解速度,求出偏转角的正切,再求粒子飞出电场时的最大偏角.
解答:解:(1)由于B板带负电,粒子向B板偏转,说明粒子带正电
(2)在粒子偏转到B板之前飞出电场.
竖直方向:
=
at2=
?t2
得:t=
水平方向:v0=
=L
=1.5×104m/s
所以要使粒子能飞出电场,粒子飞入电场时的速度v0至少为1.5×104m/s;
(3)设粒子飞出电场的最大偏角为θ,则有:tanθ=
=
=
?
=
=0.53
答:(1)粒子带正电;
(2)要使粒子能飞出电场,粒子飞入电场时的速度v0至少为1.5×104m/s.
(3)粒子飞出电场时的最大偏角正切值0.53.
(2)在粒子偏转到B板之前飞出电场.
竖直方向:
| d |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
得:t=
| md |
| qE |
水平方向:v0=
| L |
| t |
| qE |
| md |
所以要使粒子能飞出电场,粒子飞入电场时的速度v0至少为1.5×104m/s;
(3)设粒子飞出电场的最大偏角为θ,则有:tanθ=
| vy |
| v0 |
| at |
| v0 |
| qE |
| m |
| L | ||
|
| 1×10-16×4×102×0.3 |
| 1×10-22×(1.5×104)2 |
答:(1)粒子带正电;
(2)要使粒子能飞出电场,粒子飞入电场时的速度v0至少为1.5×104m/s.
(3)粒子飞出电场时的最大偏角正切值0.53.
点评:本题是带电粒子在电场中做类平抛运动的问题,关键在于分析临界条件.

练习册系列答案
相关题目
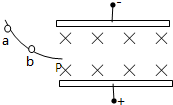 如图所示,两带电平行金属板水平放置,板间匀强磁场方向垂直纸面向里,某带电小球从光滑绝缘轨道上的a点自由滑下,经过轨道端点P进入板间后恰能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则在两板间的运动过程中( )
如图所示,两带电平行金属板水平放置,板间匀强磁场方向垂直纸面向里,某带电小球从光滑绝缘轨道上的a点自由滑下,经过轨道端点P进入板间后恰能沿水平方向作直线运动.现使小球从较低的b点开始下滑,经P点进入板间,则在两板间的运动过程中( )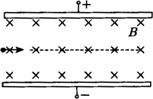
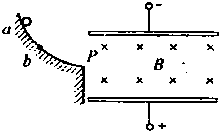
 如图所示,两带电平行金属板A、B间的电场为匀强电场,场强E=4.0×102V/m,两板相距d=16cm,板长L=30cm.一带电量q=1.0×10-16C、质量m=1.0×10-22㎏的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转,不计带电粒子所受重力,(tan28°=0.53)求:
如图所示,两带电平行金属板A、B间的电场为匀强电场,场强E=4.0×102V/m,两板相距d=16cm,板长L=30cm.一带电量q=1.0×10-16C、质量m=1.0×10-22㎏的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转,不计带电粒子所受重力,(tan28°=0.53)求: