题目内容
 (2013?厦门一模)如图所示,光滑轨道ABCD固定在竖直平面内,由直轨道AB与圆弧轨道BCD平滑相切对接组成.圆弧的圆心为O点,半径大小为R,OB与竖直方向OC夹角θ=37°,D点与圆心O点等高;竖直且过B点的直线PQ右侧空间内,被水平且过O点、D点的直线MN分为下区域Ⅰ和上区域Ⅱ,下区域Ⅰ内存在水平向右的匀强电场,场强为
(2013?厦门一模)如图所示,光滑轨道ABCD固定在竖直平面内,由直轨道AB与圆弧轨道BCD平滑相切对接组成.圆弧的圆心为O点,半径大小为R,OB与竖直方向OC夹角θ=37°,D点与圆心O点等高;竖直且过B点的直线PQ右侧空间内,被水平且过O点、D点的直线MN分为下区域Ⅰ和上区域Ⅱ,下区域Ⅰ内存在水平向右的匀强电场,场强为| E | 1 |
| E | 2 |
| E | 1 |
| mg |
| q |
| E | 2 |
| 3mg |
| 4q |
(1)小滑块滑到C点时对轨道压力大小;
(2)小滑块离开D点后,运动到与D点等高时,距D点的水平距离;
(3)小滑块离开D点后,在区域Ⅱ运动过程中,经多长时间,它所受合外力的瞬时功率最小.
分析:根据动能定理求出C点的速度,然后根据牛顿第二定律求出在C点所受支持力,根据牛顿第三定律求对轨道的压力;
解答:解:(1)小滑块在C点:FC-mg=m
小滑块A→C:mg?2r+qE1?Rsinθ=
mvc2
已知qE1=mg,解得:Fc=6.2mg
由牛顿第三定律FC′=6.2mg
(2)小滑块从A→D:
mg?r+qE1?R(1+sinθ)=
mvD2
解得:vD=
小滑块离开D点后,竖直方向做竖直上抛运动,垂直直面向里的水平方向做初速度为0的匀加速直线运动
竖直方向:t=
=2
水平方向:a=
=
g
s=
at2
解得:s=7.8R
(3)当qE2与mg的合力方向与v方向垂直时,合外力的瞬时功率最小,等于零,此时v方向与水平夹角为37°
设经过的时间为t,
vx=at=
gt
vy=vD-gt
=tan37°=
解得:t=
答:(1)小滑块滑到C点时对轨道压力大小为6.2mg;
(2)小滑块离开D点后,运动到与D点等高时,距D点的水平距离为7.8R;
(3)小滑块离开D点后,在区域Ⅱ运动过程中,经时间
,它所受合外力的瞬时功率最小.
| vc2 |
| R |
小滑块A→C:mg?2r+qE1?Rsinθ=
| 1 |
| 2 |
已知qE1=mg,解得:Fc=6.2mg
由牛顿第三定律FC′=6.2mg
(2)小滑块从A→D:
mg?r+qE1?R(1+sinθ)=
| 1 |
| 2 |
解得:vD=
| 5.2gR |
小滑块离开D点后,竖直方向做竖直上抛运动,垂直直面向里的水平方向做初速度为0的匀加速直线运动
竖直方向:t=
| 2vD |
| g |
|
水平方向:a=
| qE2 |
| m |
| 3 |
| 4 |
s=
| 1 |
| 2 |
解得:s=7.8R
(3)当qE2与mg的合力方向与v方向垂直时,合外力的瞬时功率最小,等于零,此时v方向与水平夹角为37°
设经过的时间为t,
vx=at=
| 3 |
| 4 |
vy=vD-gt
| vy |
| vx |
| 3 |
| 4 |
解得:t=
| 16 |
| 25 |
|
答:(1)小滑块滑到C点时对轨道压力大小为6.2mg;
(2)小滑块离开D点后,运动到与D点等高时,距D点的水平距离为7.8R;
(3)小滑块离开D点后,在区域Ⅱ运动过程中,经时间
| 16 |
| 25 |
|
点评:本题考查了带电物体在复合场中的运动,关键是弄清个阶段的运动形式选取相应的规律列方程求解.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 (2013?厦门一模)如图所示,有一个人站在超市的自动电梯(斜面电梯)上,若人和电梯一起斜向下匀速运动,则电梯对此人的作用力为( )
(2013?厦门一模)如图所示,有一个人站在超市的自动电梯(斜面电梯)上,若人和电梯一起斜向下匀速运动,则电梯对此人的作用力为( )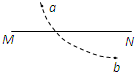 (2013?厦门一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子不计重力从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )
(2013?厦门一模)如图所示,MN是一负点电荷产生的电场中的一条电场线.一个带正电的粒子不计重力从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( ) (2013?厦门一模)下列四幅图的有关说法中正确的是( )
(2013?厦门一模)下列四幅图的有关说法中正确的是( ) (2013?厦门一模)如图所示的远距离输电电路图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压及输电线的电阻均不变.在用电高峰期,随着发电厂输出功率的增大,下列说法正确的有( )
(2013?厦门一模)如图所示的远距离输电电路图中,升压变压器和降压变压器均为理想变压器,发电厂的输出电压及输电线的电阻均不变.在用电高峰期,随着发电厂输出功率的增大,下列说法正确的有( )