题目内容
 在竖直平面内有一个粗糙的
在竖直平面内有一个粗糙的| 1 | 4 |
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到轨道最低点时,对轨道的压力大小;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功.
分析:(1)小滑块离开轨道后做平抛运动,设运动时间为t,初速度为v,根据平抛运动的基本公式即可求解;
(2)小滑块到达轨道最低点时,受重力和轨道对它的弹力,其合力充当向心力,根据牛顿第二定律即可求得轨道的支持力,即可求出滑块对轨道的压力大小;
(3)在滑块从轨道的最高点到最低点的过程中,根据动能定理即可求解克服摩擦力做功.
(2)小滑块到达轨道最低点时,受重力和轨道对它的弹力,其合力充当向心力,根据牛顿第二定律即可求得轨道的支持力,即可求出滑块对轨道的压力大小;
(3)在滑块从轨道的最高点到最低点的过程中,根据动能定理即可求解克服摩擦力做功.
解答:解:(1)解:(1)小滑块离开轨道后做平抛运动,设运动时间为t,初速度为v,则
x=vt
h=
gt2
解得:v=2.0m/s
(2)小滑块到达轨道最低点时,受重力和轨道对它的弹力为N,根据牛顿第二定律:
N-mg=m
解得:N=2.0N
根据牛顿第三定律,轨道受到的压力大小N'=N=2.0N,方向竖直向下
(3)在滑块从轨道的最高点到最低点的过程中,根据动能定理:
mgR+Wf=
mv2-0
Wf=-0.2J
所以小滑块克服摩擦力做功为0.2J.
答:(1)小滑块离开轨道时的速度大小为2m/s;
(2)小滑块运动到轨道最低点时,对轨道的压力大小为2N;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功为0.2J.
x=vt
h=
| 1 |
| 2 |
解得:v=2.0m/s
(2)小滑块到达轨道最低点时,受重力和轨道对它的弹力为N,根据牛顿第二定律:
N-mg=m
| v2 |
| R |
解得:N=2.0N
根据牛顿第三定律,轨道受到的压力大小N'=N=2.0N,方向竖直向下
(3)在滑块从轨道的最高点到最低点的过程中,根据动能定理:
mgR+Wf=
| 1 |
| 2 |
Wf=-0.2J
所以小滑块克服摩擦力做功为0.2J.
答:(1)小滑块离开轨道时的速度大小为2m/s;
(2)小滑块运动到轨道最低点时,对轨道的压力大小为2N;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功为0.2J.
点评:本题主要考查了动能定理及牛顿第二定律的直接应用,知道小球离开轨道后做平抛运动,难度适中.

练习册系列答案
相关题目
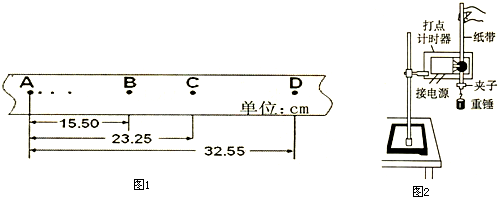

 m?2来验证机械能是否守恒
m?2来验证机械能是否守恒 来计算.其中______同学的方法更符合实验要求.重力加速度g的数值,丙同学用通过对纸带分析计算出重锤下落的实际加速度代入,丁同学用当地的实际重力加速度代入,其中______同学的做法是正确的.
来计算.其中______同学的方法更符合实验要求.重力加速度g的数值,丙同学用通过对纸带分析计算出重锤下落的实际加速度代入,丁同学用当地的实际重力加速度代入,其中______同学的做法是正确的.