Question

跳伞运动员做低空跳伞表演，他离开飞机后先做自由落体运动，当距离地面 125 m时打开降落伞，伞张开后运动员就以14.3 m/s²的加速度做匀减速运动，到达地面时速度为5 m/s，问：

（1）运动员离开飞机时距地面的高度为多少?

（2）离开飞机后，经过多少时间才能到达地面?（g=10 m/s²）

 

Answer 1

【答案】

（1）305 m. （2）9.85 s  

【解析】

试题分析：（1）离开飞机后先作自由落体运动，然后做匀减速直线运动，可根据匀加速直线运动过程中速度位移公式求出自由落体运动的末速度，再根据自由落体运动的公式求出自由落体运动的位移，两段位移之和就是运动员离开飞机时距地面的高度；

（2）分别求出自由落体运动和匀减速直线运动的时间，两者之和就是到达地面的时间．

解：（1）（5分）运动员打开伞后做匀减速运动，

由v₂²  - v₁² =2as₂可求得运动员打开伞时的速度为v₁=60 m/s           2分

运动员自由下落距离为s₁=v₁²/2g=180 m，                           2分

运动员离开飞机时距地面高度为s=s₁+s₂= 305 m.                    1分

（2）（5分）自由落体运动的时间为t₁ =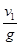= 6 s                     2分

打开伞后运动的时间为t₂=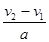=3.85 s                           2分

离开飞机后运动的时间为t=t₁+t₂=9.85 s                                      1分

考点：自由落体运动；匀变速直线运动的速度与位移的关系

点评：该题是自由落体运动和匀减速运动基本公式的直接应用，要求同学们能根据已知条件选择合适的公式进行求解，难度不大。