题目内容
 如图所示,水平传送带AB长L=12m,始终以速度v=13m/s运转,在传送带最右端B有一个与水平面成37°的斜坡.现将一个质量为m=2.0kg的小木块轻放在传送带的最左端A,小木块运动到B处就立即沿斜坡运动,但速度大小损失1/6;小木块离开坡顶C后,经过t1=0.3s垂直击中竖直挡板D.已知:小木块与传送带的之间的动摩擦因素μ1=0.6,小木块与斜坡之间的动摩擦因素μ2=0.5,重力加速度g=10m/s2.求
如图所示,水平传送带AB长L=12m,始终以速度v=13m/s运转,在传送带最右端B有一个与水平面成37°的斜坡.现将一个质量为m=2.0kg的小木块轻放在传送带的最左端A,小木块运动到B处就立即沿斜坡运动,但速度大小损失1/6;小木块离开坡顶C后,经过t1=0.3s垂直击中竖直挡板D.已知:小木块与传送带的之间的动摩擦因素μ1=0.6,小木块与斜坡之间的动摩擦因素μ2=0.5,重力加速度g=10m/s2.求(1)小木块到达传送带右端B时的速度大小
(2)小木块离开坡顶C时的速度大小
(3)小木块在斜坡上运动过程中,摩擦力对木块的冲量大小.
分析:(1)木块放在传送带上时做匀加速运动,根据动能定理求出木块滑到右端时的速度,将此速度与传送带的速度比较,再求解.
(2)将木块离开C点到D点的运动倒过来看是一个平抛运动,根据平抛运动的规律求解.
(3)由题意求出木块在斜坡底部速度大小,对于B到C过程,运用动量定理求解摩擦力对木块的冲量大小.
(2)将木块离开C点到D点的运动倒过来看是一个平抛运动,根据平抛运动的规律求解.
(3)由题意求出木块在斜坡底部速度大小,对于B到C过程,运用动量定理求解摩擦力对木块的冲量大小.
解答:解:(1)设小木块运动到右端未与皮带共速
由动能定理得:μ1mgL=
m
,
代人数据解得:v1=12m/s,小于13m/s,故小木块运动到右端速度v1=12m/s
(2)将C到D的过程倒过来看是一种平抛运动,则有:sin37°=
,得:vC=5m/s
(3)设在斜坡上运动时间为t2,在斜坡底部速度大小v2
由题意有:v2=
v1=10m/s
动量定理:-(mgsin37°+μ2mgcos37°)t2=mvC-mv2
摩擦力冲量:I=μ2mgcos37°,
解得 I=4N?s
解法二:设小木块运动x以后与皮带共速
由μ1mg=ma1…①
2a1x=v2….②
由①②得x=
>L,木块滑离B时未与皮带共速2a2x=vB2…..③
由①②③得vB=12m/s…④
(2)vy=gt…⑤vy=vcsin37°…..⑥得vc=5m/s….⑦
(3)μ2mgcos37°+mgsin37°=ma2.⑧vc=
vB-a2t2…⑨If=μ2mgcos37°?t2….⑩
由④⑦⑧⑨⑩得 If=4N?s
答:
(1)小木块到达传送带右端B时的速度大小为12m/s.
(2)小木块离开坡顶C时的速度大小为5m/s.
(3)小木块在斜坡上运动过程中,摩擦力对木块的冲量大小为4N?s.
由动能定理得:μ1mgL=
| 1 |
| 2 |
| v | 2 1 |
代人数据解得:v1=12m/s,小于13m/s,故小木块运动到右端速度v1=12m/s
(2)将C到D的过程倒过来看是一种平抛运动,则有:sin37°=
| gt1 |
| vC |
(3)设在斜坡上运动时间为t2,在斜坡底部速度大小v2
由题意有:v2=
| 5 |
| 6 |
动量定理:-(mgsin37°+μ2mgcos37°)t2=mvC-mv2
摩擦力冲量:I=μ2mgcos37°,
解得 I=4N?s
解法二:设小木块运动x以后与皮带共速
由μ1mg=ma1…①
2a1x=v2….②
由①②得x=
| 169 |
| 12 |
由①②③得vB=12m/s…④
(2)vy=gt…⑤vy=vcsin37°…..⑥得vc=5m/s….⑦
(3)μ2mgcos37°+mgsin37°=ma2.⑧vc=
| 5 |
| 6 |
由④⑦⑧⑨⑩得 If=4N?s
答:
(1)小木块到达传送带右端B时的速度大小为12m/s.
(2)小木块离开坡顶C时的速度大小为5m/s.
(3)小木块在斜坡上运动过程中,摩擦力对木块的冲量大小为4N?s.
点评:本题整合了动能定理、平抛运动、动量定理等等多个力学规律,综合性较强,关键是采用逆向思维研究C到D的过程.

练习册系列答案
相关题目
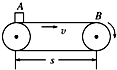 如图所示,水平传送带长为s,以速度v始终保持匀速运动,质量为m的货物无初速放到A点,货物运动到B点时恰达到速度v,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,以下说法正确的是( )
如图所示,水平传送带长为s,以速度v始终保持匀速运动,质量为m的货物无初速放到A点,货物运动到B点时恰达到速度v,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,以下说法正确的是( )A、摩擦力对物体做功为
| ||
| B、摩擦力对物体做功为μmgs | ||
| C、传送带克服摩擦力做功为μmgs | ||
| D、因摩擦而生的热能为2μmgs |
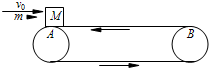 (2007?淮安模拟)如图所示,水平传送带AB长l=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度v=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求:
(2007?淮安模拟)如图所示,水平传送带AB长l=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度v=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求: 用如图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37?的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的
用如图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37?的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的 如图所示,水平传送带长为s,以速度v始终保持匀速运动,把质量为m的货物放到A点,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,摩擦力对货物做的功可能( )
如图所示,水平传送带长为s,以速度v始终保持匀速运动,把质量为m的货物放到A点,货物与皮带间的动摩擦因数为μ,当货物从A点运动到B点的过程中,摩擦力对货物做的功可能( ) 如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T,一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离磁场左边界P的距离应为多大?(g取10m/s2)
如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T,一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离磁场左边界P的距离应为多大?(g取10m/s2)