题目内容
12.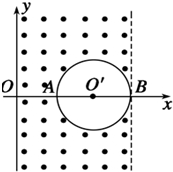 如图所示,在xOy平面内,有一个圆形区域的直径AB与x轴重合,圆心O′的坐标为(2a,0),其半径为a,该区域内无磁场.在y轴和直线x=3a之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴上某点射入磁场.不计粒子重力.则( )
如图所示,在xOy平面内,有一个圆形区域的直径AB与x轴重合,圆心O′的坐标为(2a,0),其半径为a,该区域内无磁场.在y轴和直线x=3a之间的其他区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q的带正电的粒子从y轴上某点射入磁场.不计粒子重力.则( )| A. | 若粒子的初速度方向与y轴正向的夹角为60°,且粒子不经过圆形区域就能到达B点,粒子的初速度大小为$\frac{2qBa}{m}$ | |
| B. | 若粒子的初速度方向与y轴正向的夹角为60°,且粒子不经过圆形区域就能到达B点,粒子的初速度大小为$\frac{3qBa}{m}$ | |
| C. | 若粒子的初速度方向与y轴正向的夹角为60°,在磁场中运动的时间为△t=$\frac{πm}{3Bq}$,且粒子也能到达B点,粒子的初速度大小为$\frac{3qBa}{2m}$ | |
| D. | 若粒子的初速度方向与y轴正向的夹角为60°,在磁场中运动的时间为△t=$\frac{πm}{3Bq}$,且粒子也能到达B点,粒子的初速度大小为$\frac{\sqrt{3}qBa}{2m}$ |
分析 AB、若粒子不经过圆形区域就能到达B点,故粒子到达B点时速度竖直向下,圆心必在x轴正半轴上,由几何关系确定半径,然后根据牛顿第二定律确定粒子的初速度;
CD、若粒子的初速度方向与y轴正向夹角为60°,粒子到达B点的速度与x轴夹角β=30°,由几何知识确定半径,由牛顿第二定律求粒子的初速度大小.
解答  解:AB、粒子不经过圆形区域就能到达B点,故粒子到达B点时速度竖直向下,圆心必在x轴正半轴上,设粒子做圆周运动的半径为r1,如图,由几何关系得:
解:AB、粒子不经过圆形区域就能到达B点,故粒子到达B点时速度竖直向下,圆心必在x轴正半轴上,设粒子做圆周运动的半径为r1,如图,由几何关系得:
r1sin30°=3a-r1
又qv1B=m$\frac{{v}_{1}^{2}}{{r}_{1}}$
解得:v1=$\frac{2qBa}{m}$,故A正确,B错误.
CD、粒子在磁场中的运动周期为:T=$\frac{2πm}{qB}$,故粒子在磁场中的运动轨迹的圆心角为为:α=$\frac{t}{T}$×360°=60°,粒子到达B点的速度与x轴夹角β=30°.
设粒子做圆周运动的半径为r2,由几何关系得:3a=2r2sin30°+2acos230°
又 qv2B=m$\frac{{v}_{2}^{2}}{{r}_{2}}$,解得:v2=$\frac{3qBa}{2m}$.故C正确,D错误.
故选:AC.
点评 解决本题的突破口是知道以直径为斜边的内接圆一定是直角三角形从而确定出D点的半径过A点,然后由几何关系求出圆周运动的半径从而可以顺利求解速度大小.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
2.水的折射率为n,距水面深h处有一个点光源,岸上的人看到水面被该光源照亮的圆形区域的直径为( )
| A. | 2htan(arc sin$\frac{1}{n}$) | B. | 2htan(arc sin n) | C. | 2htan(arc cos$\frac{1}{n}$) | D. | 2hcot(arc cos n) |
4. 如图所示,圆盘上叠放着两个物块A和B,当圆盘和物块绕竖直轴匀速转动时,物块与圆盘始终保持相对静止,则( )
如图所示,圆盘上叠放着两个物块A和B,当圆盘和物块绕竖直轴匀速转动时,物块与圆盘始终保持相对静止,则( )
 如图所示,圆盘上叠放着两个物块A和B,当圆盘和物块绕竖直轴匀速转动时,物块与圆盘始终保持相对静止,则( )
如图所示,圆盘上叠放着两个物块A和B,当圆盘和物块绕竖直轴匀速转动时,物块与圆盘始终保持相对静止,则( )| A. | 物块A不受摩擦力作用 | |
| B. | 物块B受5个力作用 | |
| C. | 当转速增大时,A受摩擦力增大,B受摩擦力减小 | |
| D. | A对B的摩擦力方向沿半径指向转轴 |
2.下列说法正确的是( )
| A. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是核衰变方程 | |
| B. | 10个${\;}_{92}^{238}$U原子核经过一个半衰期,必定有5个发生衰变 | |
| C. | 天然放射现象说明原子具有核式结构 | |
| D. | 波源的发射频率会随接收者的远离而降低 |
 如图所示,已知绳长l=1米,水平轻杠AC长L=1.9米,小球质量m=1kg(小球视为质点),整个装置可绕竖直转轴AB转动(AB可视为一条竖直线).当该装置以某一角速度转动时,绳子与竖直方向的夹角为θ=37°.试求该装置转动的角速度和小球需要的向心力大小.(Sin37°=0.6 cos37°=0.8 g=10m/s2,)
如图所示,已知绳长l=1米,水平轻杠AC长L=1.9米,小球质量m=1kg(小球视为质点),整个装置可绕竖直转轴AB转动(AB可视为一条竖直线).当该装置以某一角速度转动时,绳子与竖直方向的夹角为θ=37°.试求该装置转动的角速度和小球需要的向心力大小.(Sin37°=0.6 cos37°=0.8 g=10m/s2,) 如图甲所示,A、B两物体与水平面间的动摩擦因数相同,A的质量为3kg.A以一定的初速度向右滑动,与B发生碰撞(碰撞时间极短),碰前A的速度变化如图乙中图线I所示,碰后A、B的速度变化分别如图线Ⅱ、Ⅲ所示,g取10m/s2,求:
如图甲所示,A、B两物体与水平面间的动摩擦因数相同,A的质量为3kg.A以一定的初速度向右滑动,与B发生碰撞(碰撞时间极短),碰前A的速度变化如图乙中图线I所示,碰后A、B的速度变化分别如图线Ⅱ、Ⅲ所示,g取10m/s2,求:
 如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=8m/s出发向B点滑行,DB长为12m,物块与水平面间动摩擦因数μ=0.2,求:
如图所示,粗糙的水平面与竖直平面内的光滑弯曲轨道BC在B点相接.一小物块从AB上的D点以初速v0=8m/s出发向B点滑行,DB长为12m,物块与水平面间动摩擦因数μ=0.2,求: