题目内容
如图所示，质量M=2kg的滑块套在光滑的水平轨道上，质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接，小球和轻杆可在竖直平面内绕O轴自由转动，开始轻杆处于水平状态，现给小球一个竖直向上的初速度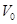
="4"
m/s，g取10
。
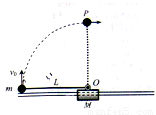
（1）若锁定滑块，试求小球通过最高点P时对轻杆的作用力大小和方向。
（2）若解除对滑块的锁定，试求小球通过最高点时的速度大小。
（3）在满足（2）的条件下，试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。
（1）2N，方向竖直向上（2）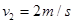
（3）
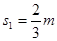
【解析】
试题分析：设小球能通过最高点，且此时的速度为v1，在上升过程中，因只有重力做功，小球的机械能守恒，则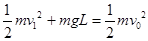
①
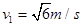②
设小球到达最高点时，轻杆对小球的作用力为F，方向向下，则小球受到的拉力和重力提供做圆周运动的向心力，有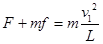
③
由②③式，得
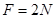④
由牛顿第三定律知，小球对轻杆的作用力大小为2N，方向竖直向上。
（2）若解除锁定，设小球通过最高点时的速度为v2，此时滑块的速度为V 。小球和滑块起始状态沿在水平方向初速度均为零，在上升过程中，因系统在水平方向不受外力作用，水平方向的动量守恒。以水平向右方向为正方向，有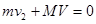
⑤
在上升过程中，因只有重力做功，系统的机械能守恒，则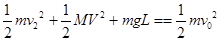
⑥，
由⑤⑥式得。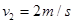
（3）设小球击中滑块右侧轨道的位置点与小球起始位置点间的距离为s1,滑块向左移动的距离为s2。任意时刻小球的水平速度大小为v3，滑块的速度大小为V‘。由系统水平方向的动量守恒，得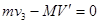
⑦将⑦式两边同乘以
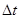，得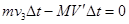
⑧，因⑧式对任意时刻附近的微小间隔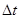都成立，累积相加后，有
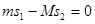⑨，又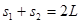
⑩,由⑨⑩式，得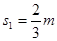m
考点：考查动量与能量
点评：本题难度较大，对于多过程问题首先应把整个运动过程分段处理，明确研究对象和过程，判断动量是否守恒、受力和做功情况
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
（2013?荆州模拟）如图所示，质量m=2.2kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动．（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
如图所示，质量m=2.0kg的木块静止在水平面上，用大小F=20N、方向与水平方向成θ=37°角的力拉动木块，当木块运动到x=10m时撤去力F．不计空气阻力．已知木块与水平面间的动摩擦因数?=0.2，sin37°=0.6，cos37°=0.8．g取10m/s2．求：
如图所示，质量m=2.0×104kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面，两桥面的圆弧半径均为20m．由于轮胎太旧，如果受到超过3×105N的压力时就会出现爆胎，则：
如图所示，质量m=2.0kg的金属块放在水平地板上，在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下，以速度v=5.0m/s向右做匀速直线运动．（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
（2013?海淀区一模）如图所示，质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的电场强度为E1的匀强电场中．取g=10m/s2．