题目内容
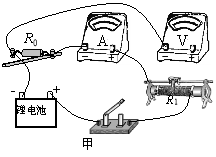
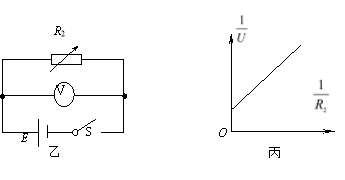
【题目】如图所示为某同学设计的投射装置，水平地面上固定一根内壁光滑的细管道，管道下端固定在水平地面上，管道竖直
部分长度为
，
部分是半径为
的四分之一圆弧，管口沿水平方向，
为圆弧的圆心。与圆心水平距离为的竖直墙壁上固定一个半径为
的圆形靶子，圆心
与等高，
为靶子的最高点和最低点。管道内
处有一插销，挡住下面的小球，弹簧上端与小球并未连接，弹簧下端固定在金属杆
上，可上下调节，改变弹簧压缩量。小球质量为
且可视为质点，不计空气阻力和弹簧的质量，重力加速度为
。为了让小球击中靶子，则:
(1)小球对管道
处的最大压力；
(2)弹簧储存的弹性势能的范围。
【答案】（1）
，方向竖直向下（2）
【解析】
（1）因管口处于水平，小球从
点离开后做平抛运动
水平位移
竖直位移
，
要使小球打到靶子上，小球下落的高度为
小球下落的时间为
，
所以小球从处离开时的速度为
当
时，轨道内侧对小球提供支持力，所以当
时，小球对轨道压力最大
由牛顿第二定律可知
解得，
由牛顿第三定律可知，小球对轨道的压力大小
压力的方向竖直向下
（2）小球由
至运动过程中，根据能量守恒可知，取所在水平面为零势能面
由此求得
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
