题目内容
如图所示，一根细绳通过定滑轮在两端分别系着A和B两物体，物体A在水平外力作用下水平向右运动，当α=60°，β=30°时，A、B两物体的速度大小之比为（ ）| A、vA：vB=1：1 | ||
B、vA：vB=
| ||
| C、vA：vB=1：2 | ||
D、vA：vB=
|
分析：分别对A、B物体速度沿着绳子方向与垂直绳子方向进行分解，根据三角函数关系及沿着绳子方向速度大小相等，可知两物体的速度大小关系．
解答：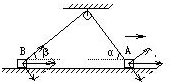
解：对A物体的速度沿着绳子方向与垂直绳子方向进行分解，则有沿着绳子方向的速度大小为：v绳=vAcosα；
对B物体的速度沿着绳子方向与垂直绳子方向进行分解，则有沿着绳子方向的速度大小为：v绳=vBcosβ，
由于沿着绳子方向速度大小相等，所以则有：vAcosα=vBcosβ，因此vA：vB=
：1．
故选：B．
解：对A物体的速度沿着绳子方向与垂直绳子方向进行分解，则有沿着绳子方向的速度大小为：v绳=vAcosα；对B物体的速度沿着绳子方向与垂直绳子方向进行分解，则有沿着绳子方向的速度大小为：v绳=vBcosβ，
由于沿着绳子方向速度大小相等，所以则有：vAcosα=vBcosβ，因此vA：vB=
| 3 |
故选：B．
点评：考查学会对物体进行运动的分解，涉及到平行四边形定则与三角函数知识，同时本题的突破口是沿着绳子的方向速度大小相等．关键的是要明确物体实际运动的速度为合速度．
练习册系列答案
相关题目
在验证“互成角度的两个力的合成”的实验中，先将橡皮条的一端固定在水平木板上，另一端系上带有绳套的两根细绳．实验时，需要两次拉伸橡皮条，一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条，另一次是用一个弹簧秤通过细绳拉橡皮条．
（1）在“探究求合力的方法”时，先将橡皮条的一端固定在水平木板上，另一端系上带有绳套的两根细绳．实验时，先后两次拉伸橡皮条，一次是用两个弹簧秤通过两细绳互成角度地拉橡皮条，另一次是用一个弹簧秤通过细绳拉橡皮条．在本实验中，下列说法正确的是
出间距d．开始时将木板置于MN处，现缓慢向瓶中加水，直到木板刚刚开始运动为止，记下弹簧秤的示数F0，以此表示滑动摩擦力的大小．再将木板放回原处并按住，继续向瓶中加水后，记下弹簧秤的示数F1，然后释放木板，并用秒表记下木板运动到PQ处的时间t． ①木板的加速度可以用d、t表示为a=
