题目内容
如图所示真空室内存在匀强磁场，磁场方向垂直纸面向里，磁感应强度
，磁场内有一块平面感光板
，板面与磁场方向平行，在距距离
处，有一个点状的
放射源
，它向各个方向发射粒子，粒子的速度都是
，已知粒子的电荷量与质量之比
，现只考虑在纸面中运动的粒子，求上被粒子打中的区域的长度。
上被粒子打中的区域的长度20cm
解析:
如图所示
所以有：
带入数据得： 
可见
因朝不同方向发射的
粒子的轨道都经过
，如图所示，某一圆轨迹在图中
点左侧与
向切，则此切点
就是粒子能打中的左侧最远点，由图中几何关系得
再考虑点右侧，任何粒子在运动过程中离点的距离不可能超过
，故图中
点即为右侧粒子能打到的最远点，由图中几何关系得
故所求的长度为
说明：本题可以以粒子源为圆心四等分圆，分析每个不部分上的运动轨迹，同时再考虑特殊的运动方向――直径方向的运动。
练习册系列答案
相关题目
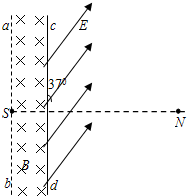如图所示，真空室内存在宽度为d=8cm的匀强磁场区域，磁感应强度B=0.332T，磁场方向垂直于纸面向里；ab、cd足够长，cd为厚度不计的金箔，金箔右侧有一匀强电场区域，电场强度E=3.32×105N/C；方向与金箔成37°角．紧挨边界ab放一点状α粒子放射源S，可沿纸面向各个方向均匀放射初速率相同的α粒子，已知：α粒子的质量m=6.64×10-27kg，电荷量q=+3.2×10-19C，初速度
在地面上方的真空室内，有一对平行金属板M、N竖直放置，两板间存在恒定的电势差，设两板间的电场可看作是匀强电场，且两板外无电场，将一电量q=4×10-6C的带电小球从两极板上方距两极板上端高度h=0.2m的A点以初动能EK0=8×10-3J水平抛出，球恰好从靠近M板上端处射入板内，然后沿直线运动并碰到N板上的B点，B点与极板上端相距L=0.15m，如图所示．
A．在一真空室内存在着匀强电场和匀强磁场，电场强度E与磁感应强度B的方向平行，已知电场强度E=40.0V/m，磁感应强度B=0.30T．如图所示，在该真空室内建立Oxyz三维直角坐标系，其中z轴竖直向上．质量m=1.0×10-4 kg，带负电的质点以速度v0=100m/s沿+x方向做匀速直线运动，速度方向与电场、磁场垂直，取g=10m/s2．
如图所示，真空室内存在匀强磁场，磁场方向垂直于纸面向里，磁感应强度的大小B=0.60T．磁场内有一块足够大的平面感光平板ab，板面与磁场方向平行．在距ab的距离为l=10cm处，有一个点状的α放射源S，它仅在纸平面内向各个方向均匀地发射α粒子．设放射源每秒发射n=3.0×104个α粒子，每个α粒子的速度都是v=6.0×106m/s．已知α粒子的电荷与质量之比