Question

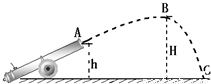
如图所示是一门古炮，炮口距地面的高度为h，当开炮后炮弹运动的轨迹如图中的虚线ABC所示，炮弹运动轨迹的最高点是B点，离地面的高度为H，落在地面的C点．若炮弹的质量为m，在B点的速度大小为V_B，忽略空气阻力的影响，重力加速度为g．
求：（1）说出B点的速度方向
（2）发射炮弹时火药对炮弹做的功
（3）炮弹落在C点时的速度大小和方向．

Answer 1

分析：（1）炮弹到达最高点，竖直方向上的分速度为零，最终速度为水平方向．
（2）对A到B的过程运用动能定理，求出炮弹在A点的动能，根据能量守恒定律求出发射炮弹时火药对炮弹做的功．
（3）根据动能定理求出C点的速度大小，根据平行四边形定则求出C点的速度方向．

解答：解：（1）B点的速度方向为水平向右
（2）炮弹由A-B的过程中，忽略空气阻力的作用，
根据动能定理有-mg（H-h）=

1

2

mv_B²-

1

2

mv_A²
又E_KA=

1

2

mv_A²
由以上各式可得 E_KA=

1

2

mv_B²+mg（H-h）
由能的转化与守恒可得，火药对炮弹做的功转化为炮弹的动能和势能．
即火药对炮弹做的功为

1

2

mv_B²+mg（H-h）+mgh=

1

2

mv_B²+mgH
（3）炮弹由B-C的过程中做平抛运动，根据动能定理可得
mgH=

1

2

mv_C²-

1

2

mv_B²
炮弹在C点的速度vC=

2gH+vB2

 
炮弹在C点的速度方向与水平方向的夹角为α，如图所示

cosα=

vB

2gH+vB2

则α=arccos

vB

2gH+vB2

．
答：（1）B点的速度方向水平向右．
（2）发射炮弹时火药对炮弹做的功

1

2

mv_B²+mgH．
（3）炮弹落在C点时的速度大小vC=

2gH+vB2

，方向与水平方向的夹角为α=arccos

vB

2gH+vB2

．

点评：本题考查动能定理的基本运用，运用动能定理解题，首先确定研究过程，分析过程中有哪些力做功，然后列式求解．