题目内容
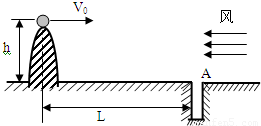
如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.无风力的作用时,高尔夫球恰好落在距击球点水平距离为2L的B洞.设重力加速度为g,求:(1)该球从击出到洞口的时间;该球被击出时初速的大小;
(2)若该球受到水平风力的作用,以相同的初速度将该球击出,高尔夫球恰好落在距击球点水平距离为L的A洞.求水平风力的大小及球落地时的速度.
【答案】分析:(1)由题意知,小球做平抛运动,水平方向作匀速运动,竖直方向自由下落;根据竖直分位移可求出运动时间,再结合水平分位移可求出初速度.
(2)由于水平方向受到风力影响,因而小球水平方向分运动改为匀减速直线运动,竖直方向分运动仍然为自由落体运动;由竖直分位移可先求出运动时间,再根据位移时间公式求出水平方向分运动加速度,结合牛顿第二定律就可求出水平风力;求出落地时的水平分速度和竖直分速度,结合平行四边形定则就可求出合速度!
解答:解:(1)根据运动的分解:高尔夫球竖直方向做自由落体运动,故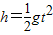 ;
;
该球从击出到洞口的时间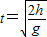 ;
;
水平方向做匀速直线运动 2L=vt;
故被击出时初速的大小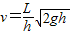 .
.
(2)有风时,水平方向做匀减速直线运动,有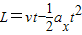 ,得到,
,得到,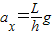 ;
;
故水平风力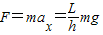 ;
;
落地时水平分速度为 vx=v-axt=0,落地时竖直分速度为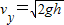 ;
;
故落地时的速度大小为: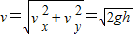 ,方向竖直向下.
,方向竖直向下.
点评:解决运动的合成与分解类问题,要注意两分运动同时发生(等时性),互不干扰(独立性),分运动与合运动可相互等效替代(等效性);本题中水平方向的力改变水平方向的速度,对竖直分运动不产生影响;同理,竖直方向的重力只改变竖直方向的速度,对水平分运动也无影响!
(2)由于水平方向受到风力影响,因而小球水平方向分运动改为匀减速直线运动,竖直方向分运动仍然为自由落体运动;由竖直分位移可先求出运动时间,再根据位移时间公式求出水平方向分运动加速度,结合牛顿第二定律就可求出水平风力;求出落地时的水平分速度和竖直分速度,结合平行四边形定则就可求出合速度!
解答:解:(1)根据运动的分解:高尔夫球竖直方向做自由落体运动,故
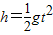 ;
; 该球从击出到洞口的时间
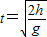 ;
;水平方向做匀速直线运动 2L=vt;
故被击出时初速的大小
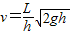 .
.(2)有风时,水平方向做匀减速直线运动,有
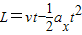 ,得到,
,得到,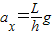 ;
; 故水平风力
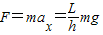 ;
;落地时水平分速度为 vx=v-axt=0,落地时竖直分速度为
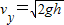 ;
;故落地时的速度大小为:
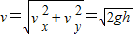 ,方向竖直向下.
,方向竖直向下.点评:解决运动的合成与分解类问题,要注意两分运动同时发生(等时性),互不干扰(独立性),分运动与合运动可相互等效替代(等效性);本题中水平方向的力改变水平方向的速度,对竖直分运动不产生影响;同理,竖直方向的重力只改变竖直方向的速度,对水平分运动也无影响!

练习册系列答案
相关题目
 随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则下列判断中错误的是( )
随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则下列判断中错误的是( )| A、球被击出后做平抛运动 | ||||
B、该球从被击出到落入A穴所用的时间为
| ||||
C、球被击出时的初速度大小为L
| ||||
D、球被击出后受到的水平风力的大小为
|
 随着人们生活水平的提高,打高尔夫球将逐渐成为普通人的休闲娱乐方式.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则( )
随着人们生活水平的提高,打高尔夫球将逐渐成为普通人的休闲娱乐方式.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则( )| A、球被击出后做平抛运动 | ||||||
B、该球从被击出到落入A穴所用的时间为
| ||||||
C、球被击出时的初速度大小为
| ||||||
D、球被击出后受到的水平风力的大小为
|
 随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.
随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴. (2011?山西二模)如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球,由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴,则( )
(2011?山西二模)如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球,由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴,则( ) 随着人们生活水平的提高,打高尔夫球将逐渐成为普通人的休闲娱乐方式.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则( )
随着人们生活水平的提高,打高尔夫球将逐渐成为普通人的休闲娱乐方式.如图所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直地落入距击球点水平距离为L的A穴.则( )