题目内容
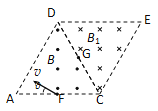
【题目】如图所示，纸面内两个边长均为L的正三角形ΔACD、ΔDEC构成一个棱形，ΔACD区域内有垂直于纸面向外的匀强磁场，磁感应强度大小为B，ΔDEC区域内有垂直于纸面向里的匀强磁场。一质量为m、电荷量为q的带正电粒子从AC边的中点F沿与FA成θ＝30°的方向射入ΔACD区域，从DC边的中点G离开ΔACD区域进入ΔDEC区域。不计粒子重力，求：
(1)粒子射入磁场时速度v的大小；
(2)要使粒子不从CE边飞出，ΔDEC区域内磁场的磁感应强度B1的最小值。
【答案】（1）
（2）
【解析】
(1)由根据带电粒子在匀强磁场中做匀速圆周运动的特点及几何知识可知，粒子在△ACD区域内做匀速圆周运动的轨道半径：
由洛伦兹力公式得：
由匀速圆周运动得：
联立以上公式得：
(2)由根据带电粒子在匀强磁场中做匀速圆周运动的特点及几何知识可知，粒子在△CDE区域中不从CE边飞出的最大轨道半径：
由洛伦兹力公式得：
由匀速圆周运动得：
联立以上公式得：
练习册系列答案
相关题目
