题目内容
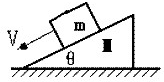如图所示，放置在水平地面上的直角劈M上有一个质量为m的物体，若m在直角劈上面匀加速下滑，M仍保持静止，那么正确的说法是（ ）| A、M对地面的压力等于（M+m）g | B、M对地面的压力大于（M+m）g | C、地面对M没有摩擦力 | D、地面对M有向左的摩擦力 |
分析：分别对M和m受力分析，然后沿水平方向和竖直方向进行正交分解，抓住M所受合力为零，根据牛顿第二定律，结合共点力平衡进行分析．
解答：解：
对m分析，m受重力、支持力和摩擦力，因为m加速下滑，具有沿斜面向下的加速度，将该加速度沿水平方向和竖直方向分解．则m支持力在水平方向上的分力大于摩擦力在水平方向上的分力，支持力和摩擦力在竖直方向分力之和小于m的重力．
对M分析，M对m的支持力和摩擦力与m对M的压力和摩擦力大小相等．则N2在水平方向上的分力大于f2在水平方向上的分力，根据水平方向上平衡，知地面对M的摩擦力向左．因为f2和N2在竖直方向上的分力之和小于m的重力，根据M在竖直方向上平衡知，地面的支持力小于（M+m）g．故D正确，A、B、C错误．
故选：D．
对m分析，m受重力、支持力和摩擦力，因为m加速下滑，具有沿斜面向下的加速度，将该加速度沿水平方向和竖直方向分解．则m支持力在水平方向上的分力大于摩擦力在水平方向上的分力，支持力和摩擦力在竖直方向分力之和小于m的重力．对M分析，M对m的支持力和摩擦力与m对M的压力和摩擦力大小相等．则N2在水平方向上的分力大于f2在水平方向上的分力，根据水平方向上平衡，知地面对M的摩擦力向左．因为f2和N2在竖直方向上的分力之和小于m的重力，根据M在竖直方向上平衡知，地面的支持力小于（M+m）g．故D正确，A、B、C错误．
故选：D．
点评：解决本题的关键能够正确地受力分析，运用牛顿第二定律和共点力平衡综合求解．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
如图所示，放置在水平地面上的质量为M的直角劈上有一个质量为m的物体，若物体在其上匀速下滑，直角劈仍保持静止，那么下列说法正确的是（ ）
如图所示，放置在水平地面质量为M的直角劈上，有一个质量为m的物体沿斜面加速下滑，M保持静止，则下列说法正确的是（ ）
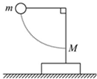如图所示，放置在水平地面上的支架质量为M，支架顶端用细线拴着的摆球质量为m，现将摆球拉至水平位置，而后释放，摆球运动过程中，支架始终不动，以下说法正确的是（ ）
| A、在释放前的瞬间，支架对地面的压力为（m+M）g | B、在释放前的瞬间，支架对地面的压力为mg | C、摆球到达最低点时，支架对地面的压力为（m+M）g | D、摆球到达最低点时，支架对地面的压力为（3m+M）g |
如图所示，放置在水平地面上的斜面，有一个物体A静止子上面，现用一竖直向下的外力F作用于A，下列说法中正确的是（ ）