题目内容
4. 如图所示,两个质量相同的物体从A点静止释放,分别沿光滑面AB与AC滑到同一水平面上的B点与C点,则下列说法中正确的是( )
如图所示,两个质量相同的物体从A点静止释放,分别沿光滑面AB与AC滑到同一水平面上的B点与C点,则下列说法中正确的是( )| A. | 两物体到达斜面底端时的速度相同 | |
| B. | 两物体到达斜面底端时的动能相同 | |
| C. | 两物体沿AB面和AC面运动时间相同 | |
| D. | 两物体从释放至到达斜面底端过程中,重力的平均功率相同 |
分析 由于斜面光滑,由动能定理可以判定到底端的速度和动能;对物体受力分析,求得加速度,然后列位移时间关系式计算时间,再根据功率公式即可求得平均功率.
解答 解:AB、斜面光滑,做功的只有重力,由于从同一位移下滑达到同一平面,故重力做功相同,由机械能守恒定律可知,动能变化相同,故到底端的动能相同,但是由于速度方向不一样,故速度不相同.故A错误,B正确
C、物体沿斜面向下的合力为:F=mgsinθ,故其加速度为:a=$\frac{mgsinθ}{m}$=gsinθ,位移为:x=$\frac{h}{sinθ}$,由位移时间关系:x=$\frac{1}{2}$at2
得:$\frac{h}{sinθ}$=$\frac{1}{2}$gsinθt2
解得:t=$\sqrt{\frac{2h}{gsi{n}^{2}θ}}$
沿AB的θ角小,故沿AB的运动时间长.故C错误;
D、因重力做功相同,但用时不等,则由P=$\frac{W}{t}$可知,重力做功的平均功率不相同,故D错误.
故选:B
点评 本题考查机械能守恒定律的应用,要注意AB两个选项利用功能关系进行分析更为简单方便,而不是用运动学来解,运动也能解,但是要麻烦一些.

练习册系列答案
相关题目
15.下列说法正确的是( )
| A. | 平抛运动的物体速度变化量的方向始终是竖直向下的 | |
| B. | 做圆周运动的物体所受各力的合力一定等于向心力 | |
| C. | 两个速率不等的匀速直线运动的合运动一定是曲线运动 | |
| D. | 曲线运动不可能是一种匀变速运动 |
12.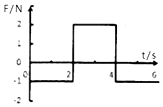 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力随时间t变化的图象如图所示,则下列说法中不正确的是( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力随时间t变化的图象如图所示,则下列说法中不正确的是( )
 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力随时间t变化的图象如图所示,则下列说法中不正确的是( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力随时间t变化的图象如图所示,则下列说法中不正确的是( )| A. | 0~6s内拉力做的功为零 | B. | 2~4s内拉力对物体做功为零 | ||
| C. | 6s末物体的动量为零 | D. | 2~4s内拉力对物体的冲量为零 |
17.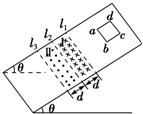 如图所示,在倾角为θ的光滑斜面上,有三条水平虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ宽度均为d,两区域分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框,从l1上方一定高度处由静止开始沿斜面下滑,当ab边刚越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )
如图所示,在倾角为θ的光滑斜面上,有三条水平虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ宽度均为d,两区域分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框,从l1上方一定高度处由静止开始沿斜面下滑,当ab边刚越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )
 如图所示,在倾角为θ的光滑斜面上,有三条水平虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ宽度均为d,两区域分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框,从l1上方一定高度处由静止开始沿斜面下滑,当ab边刚越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )
如图所示,在倾角为θ的光滑斜面上,有三条水平虚线l1、l2、l3,它们之间的区域Ⅰ、Ⅱ宽度均为d,两区域分别存在垂直斜面向下和垂直斜面向上的匀强磁场,磁感应强度大小均为B,一个质量为m、边长为d、总电阻为R的正方形导线框,从l1上方一定高度处由静止开始沿斜面下滑,当ab边刚越过l1进入磁场Ⅰ时,恰好以速度v1做匀速直线运动;当ab边在越过l2运动到l3之前的某个时刻,线框又开始以速度v2做匀速直线运动,重力加速度为g.在线框从释放到穿出磁场的过程中,下列说法正确的是( )| A. | 线框中感应电流的方向不变 | |
| B. | 线框ab边从l1运动到l2所用时间大于从l2运动到l3所用时间 | |
| C. | 线框以速度v2做匀速直线运动时,发热功率为$\frac{{m}^{2}{g}^{2}R}{4{B}^{2}{d}^{2}}$sin2θ | |
| D. | 线框从ab边进入磁场到速度变为v2的过程中,减少的机械能△E机与重力做功WG的关系式是△E机=WG+$\frac{1}{2}$mv12-$\frac{1}{2}$mv22 |
18.如图所示,矩形闭合导线与匀强磁场垂直,一定产生感应电流的是( )


| A. | 垂直于纸面平动 | B. | 以一条边为轴转动 | ||
| C. | 沿与磁场垂直的方向平动 | D. | 以上都能产生感应电流 |
 在如图所示的轻滑轮上跨有一轻绳,绳的两端连接着质量分别为1kg和2kg的物体A和B.现以50N的恒力F向上提滑轮的轴,不计滑轮质量及滑轮与绳间摩擦,求A和B的加速度各为多少?
在如图所示的轻滑轮上跨有一轻绳,绳的两端连接着质量分别为1kg和2kg的物体A和B.现以50N的恒力F向上提滑轮的轴,不计滑轮质量及滑轮与绳间摩擦,求A和B的加速度各为多少? 如图所示,为室内冰雪乐园中一个游玩项目,倾斜冰面与水平面夹角θ=30°,冰面长、宽均为L=40m,倾斜冰面两侧均安装有安全网护栏,在冰面顶端中点,由工作人员负责释放载有人的凹形滑板,与冰面相连的水平面上安有缓冲装置(图中未画出),使滑下者能安全停下.周末某父子俩前往游玩,设父亲与滑板总质量为M=80kg,儿子与滑板总质量为m=40kg,父子俩准备一起下滑,在工作人员静止释放的瞬间,父亲沿水平方向推了一下儿子,父子俩迅速分开,并沿冰面滑下.不计一切阻力,重力加速度g取10m/s2,父子俩均视为质点.
如图所示,为室内冰雪乐园中一个游玩项目,倾斜冰面与水平面夹角θ=30°,冰面长、宽均为L=40m,倾斜冰面两侧均安装有安全网护栏,在冰面顶端中点,由工作人员负责释放载有人的凹形滑板,与冰面相连的水平面上安有缓冲装置(图中未画出),使滑下者能安全停下.周末某父子俩前往游玩,设父亲与滑板总质量为M=80kg,儿子与滑板总质量为m=40kg,父子俩准备一起下滑,在工作人员静止释放的瞬间,父亲沿水平方向推了一下儿子,父子俩迅速分开,并沿冰面滑下.不计一切阻力,重力加速度g取10m/s2,父子俩均视为质点.

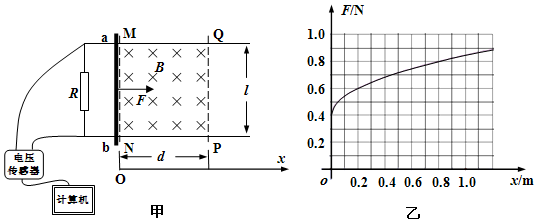 如图甲所示,光滑的平行金属导轨水平放置,导轨间距L=1m,左侧接一阻值为R=0.5Ω的电阻.在MN与PQ之间存在垂直轨道平面的有界匀强磁场,磁场宽度d=1m.一质量m=1kg的金属棒ab置于导轨上,与导轨垂直且接触良好,不计导轨和金属棒的电阻.金属棒ab受水平力F的作用从磁场的左边界MN由静止开始运动,其中,F与x(x为金属棒距MN的距离)的关系如图乙所示.通过电压传感器测得电阻R两端电压随时间均匀增大.则:
如图甲所示,光滑的平行金属导轨水平放置,导轨间距L=1m,左侧接一阻值为R=0.5Ω的电阻.在MN与PQ之间存在垂直轨道平面的有界匀强磁场,磁场宽度d=1m.一质量m=1kg的金属棒ab置于导轨上,与导轨垂直且接触良好,不计导轨和金属棒的电阻.金属棒ab受水平力F的作用从磁场的左边界MN由静止开始运动,其中,F与x(x为金属棒距MN的距离)的关系如图乙所示.通过电压传感器测得电阻R两端电压随时间均匀增大.则: