题目内容
如图所示，在xoy坐标系第一象限内有一个与x轴相切于Q点的有理想边界圆形匀强磁场，磁感应强度为B，方向垂直纸面向外，一带电粒子（不计重力）质量为m，带电荷量为+q，以初速度v0从P点进入第一象限，已知θ=30°．经过该圆形有界磁场时．速度方向改变了α=60°，并从x轴上的Q点射出．试求：（1）该圆形磁场区域的半径R；
（2）该粒子在磁场中的运动时间t．
（3）使带电粒子不能穿过x轴时圆形磁场区域的最小半径r．
分析：（1）可以通过几何关系求出粒子做圆周运动的半径和轨迹圆半径的关系，再根据圆周运动的半径公式即可求解；
（2）可先求圆弧对应的圆心角，根据圆心角和周期之间的关系及周期公式求解；
（3）带电粒子不能穿过x轴时圆形磁场区域，跟x轴相切时半径最小，根据几何关系及圆周运动的半径公式即可求解．
（2）可先求圆弧对应的圆心角，根据圆心角和周期之间的关系及周期公式求解；
（3）带电粒子不能穿过x轴时圆形磁场区域，跟x轴相切时半径最小，根据几何关系及圆周运动的半径公式即可求解．
解答：解：（1）如下图所示：
设粒子从A点射入磁场，连QA得弦，因速度偏转角为60°，那么弦切角就为30°，可知弦QA平行于y轴，又因为磁场区域圆在Q点与x轴相切，因此，AQ也是区域圆的直径；而粒子在磁场中转过的圆心角为α=60°，可知△AO'Q为等边三角形，有：2R=r（r为轨迹圆半径）
又因为r=
所以圆形磁场区域的半径为R=
．
（2）T=
圆弧对应的圆心角α=60°
t=
T=
=
．
（3）因为第一小题中已求得：
r=
如下图所示：
R=rcosa=rcos30°
R=
r=
．
答：（1）该圆形磁场区域的半径为R=
；
（2）该粒子在磁场中的运动时间为
；
（3）使带电粒子不能穿过x轴时圆形磁场区域的最小半径为
．
设粒子从A点射入磁场，连QA得弦，因速度偏转角为60°，那么弦切角就为30°，可知弦QA平行于y轴，又因为磁场区域圆在Q点与x轴相切，因此，AQ也是区域圆的直径；而粒子在磁场中转过的圆心角为α=60°，可知△AO'Q为等边三角形，有：2R=r（r为轨迹圆半径）
又因为r=
| mv0 |
| Bq |
所以圆形磁场区域的半径为R=
| mv0 |
| 2qB |
（2）T=
| 2πm |
| Bq |
圆弧对应的圆心角α=60°
t=
| α |
| 2π |
| T |
| 6 |
| πm |
| 3Bq |
（3）因为第一小题中已求得：
r=
| mv0 |
| Bq |
如下图所示：
R=rcosa=rcos30°
R=
| ||
| 2 |
| ||
| 2Bq |
答：（1）该圆形磁场区域的半径为R=
| mv0 |
| 2qB |
（2）该粒子在磁场中的运动时间为
| πm |
| 3Bq |
（3）使带电粒子不能穿过x轴时圆形磁场区域的最小半径为
| ||
| 2Bq |
点评：该题主要考查带电粒子在磁场中运动的半径及周期公式的应用，难度较大．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在竖直平面的xOy坐标系中，Oy竖直向上，Ox水平．设平面内存在沿x轴正方向的恒定风力．一物体从坐标原点沿Oy方向竖直向上抛出，初速度为v0=4m/s，不计空气阻力，到达最高点的位置如图中M点所示，（坐标格为正方形，g=10m/s2）
如图所示，在竖直平面的xoy坐标系中，oy竖直向上，ox水平．该平面内存在沿x轴正方向的恒定风力．一物体从坐标原点沿oy方向竖直向上抛出，初速度为V0=4m/s，不计空气阻力，到达最高点的位置如图中M点所示，（坐标格为正方形）求：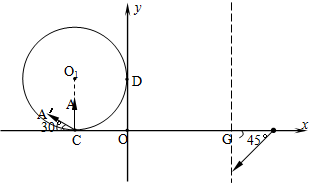
D点进入电场，最后从G点以与x轴正向夹角为45°的方向射出电场．求：
