题目内容
已知函数 和
和 的图象关于
的图象关于 轴对称,且
轴对称,且 .
.
(1)求函数 的解析式;
的解析式;
(2)解不等式 .
.
【答案】
(1) 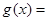
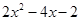 .
(2)
.
(2) 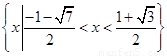 .
.
【解析】
试题分析:(1)利用“代入法(或相关点法)”设函数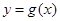 图象上任意一点
图象上任意一点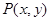 ,
,
由已知点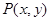 关于
关于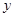 轴对称点
轴对称点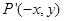 一定在函数
一定在函数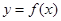 图象上,
图象上,
代入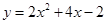 ,即得所求.
,即得所求.
(2) 将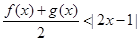 化为
化为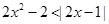 ,
,
通过分类讨论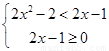 或
或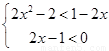 求得不等式的解集.
求得不等式的解集.
试题解析:(1)设函数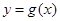 图象上任意一点
图象上任意一点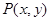 ,
,
由已知点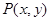 关于
关于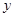 轴对称点
轴对称点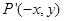 一定在函数
一定在函数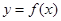 图象上, 2分
图象上, 2分
代入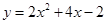 ,得
,得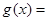
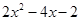 .
4分
.
4分
(2) 由(1)知不等式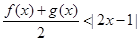 可化为
可化为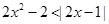 ,
,
即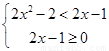 或
或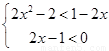 8分
8分
解得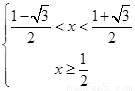 或
或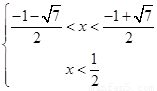 10分
10分
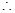
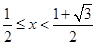 或
或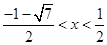
 原不等式的解集是
原不等式的解集是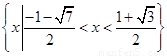 . 12分
. 12分
考点:轨迹方程求法(代入法、相关点法),简单不等式的解法.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目







