��Ŀ����
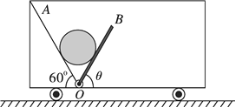
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵxoy�еĵ�һ�����ڴ��ڴŸ�Ӧǿ�ȴ�СΪB������ֱ������ƽ��������н�Բ����ǿ�ų�����(ͼ��δ����)���ڵڶ������ڣ�������x�Ḻ�������=30������ǿ�糡��һ����Դ�̶���X��������Ϊ(-L��0)��A�㡣����Դ��y���������ͷų�����Ϊm�������Ϊ-q���ٶȴ�СΪv�Ĵ������ӣ����Ӵ�ֱy��ͨ��C������һ���ޣ��־����ų�ƫת��ֱx������������(�������ӵ���������)����:

(1)��ǿ�糡�ĵ糡ǿ��E�Ĵ�С��
(2)���������뿪�糡ʱ���ٶȴ�С��
(3)Բ����ǿ�ų�����С���.
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
��������
����ţ�ٵڶ����ɵõ�ˮƽ����ֱ����ļ��ٶȣ�Ȼ�������˶�ѧ����⼴�ɣ�
�������������ṩ�����������켣�İ뾶��ȷ���ų�����С�뾶���õ���С�����
��1����A��C�Ĺ����У���x�᷽�����ţ�ٵڶ����ɵõ���![]()
��x�᷽���ȼ����˶�����![]()
��y�᷽�����ţ�ٵڶ����ɵõ���![]() ��
��
��y�᷽���ȼ����˶�����![]()
�������Եõ���![]()
��2�������뿪�糡ʱ���ٶ�Ϊ![]() ���У�
����![]() ��
��![]()
��ã�![]() ��
��
��3�������ڴų�����Բ���˶��İ뾶Ϊ![]() ��
��![]() ����
����![]()
��Բ�δų�����С���Ϊ![]() ����
����![]() ��
��

��ϰ��ϵ�д�
�����Ŀ