题目内容
3.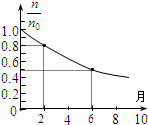 如图所示为某种放射性元素的衰变规律(纵坐标$\frac{n}{{n}_{0}}$表示任意时刻放射性元素的原子数与t=0时的原子数之比),则该放射性元素的半衰期是180天(一个月按30天计算).在从某古迹中发掘出来的木材中,所含${\;}_{6}^{14}$C的比例是正在生长的植物中的80%,放射性${\;}_{6}^{14}$C的半衰期是5700年,根据图象可以推算,该古迹距今约1900年.
如图所示为某种放射性元素的衰变规律(纵坐标$\frac{n}{{n}_{0}}$表示任意时刻放射性元素的原子数与t=0时的原子数之比),则该放射性元素的半衰期是180天(一个月按30天计算).在从某古迹中发掘出来的木材中,所含${\;}_{6}^{14}$C的比例是正在生长的植物中的80%,放射性${\;}_{6}^{14}$C的半衰期是5700年,根据图象可以推算,该古迹距今约1900年.
分析 根据半衰期的定义:原子核有半数衰变所需要的时间,由图象读出该放射性元素的半衰期.由题,古迹中发掘出来的木材中,所含C14的比例是正在生长的植物中的80%,可求出该古迹距今约的年代.
解答 解:根据半衰期的意义,$\frac{n}{{n}_{0}}$=0.5时,对应的时间即为一个半衰期,由图象可知该放射性元素的半衰期是6个月,即为180天.
由图象反映的信息可知,当$\frac{n}{{n}_{0}}$=0.8时,对应的时间为$\frac{1}{3}$个半衰期,由C14的半衰期是5700年,得该古迹距今约1900年.
故答案为:180,1900
点评 本题关键要理解并掌握半衰期的意义,会应用半衰期的公式M=M0${(\frac{1}{2})}^{\frac{t}{T}}$,考查读图能力.

练习册系列答案
相关题目
13. 如图所示,水平放置的金属导轨MN和PQ上放置AB和CD两根细铜棒,在导轨之间存在磁场,当CD棒向右运动时,下列说法正确的是( )
如图所示,水平放置的金属导轨MN和PQ上放置AB和CD两根细铜棒,在导轨之间存在磁场,当CD棒向右运动时,下列说法正确的是( )
 如图所示,水平放置的金属导轨MN和PQ上放置AB和CD两根细铜棒,在导轨之间存在磁场,当CD棒向右运动时,下列说法正确的是( )
如图所示,水平放置的金属导轨MN和PQ上放置AB和CD两根细铜棒,在导轨之间存在磁场,当CD棒向右运动时,下列说法正确的是( )| A. | CD中有感应电流产生,方向由C向D | B. | CD中有感应电流产生,方向由D向C | ||
| C. | CD中没有感应电流产生 | D. | 以上说法都不对 |
14. 两条导线互相垂直,如图所示,但相隔一段小距离,其中一条AB是固定的,另一条CD能自由活动,当直流电流按图方向通与两条导线时,导线CD将(从纸外向纸内看)( )
两条导线互相垂直,如图所示,但相隔一段小距离,其中一条AB是固定的,另一条CD能自由活动,当直流电流按图方向通与两条导线时,导线CD将(从纸外向纸内看)( )
 两条导线互相垂直,如图所示,但相隔一段小距离,其中一条AB是固定的,另一条CD能自由活动,当直流电流按图方向通与两条导线时,导线CD将(从纸外向纸内看)( )
两条导线互相垂直,如图所示,但相隔一段小距离,其中一条AB是固定的,另一条CD能自由活动,当直流电流按图方向通与两条导线时,导线CD将(从纸外向纸内看)( )| A. | 顺时针方向转动,同时靠近导线AB | B. | 逆时针方向转动,同时靠近导线AB | ||
| C. | 逆时针方向转动,同时离开导线AB | D. | 顺时针方向转动,同时离开导线AB |
8. 粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m1和m2的木块,m1>m2,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )
粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m1和m2的木块,m1>m2,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )
 粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m1和m2的木块,m1>m2,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )
粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m1和m2的木块,m1>m2,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )| A. | 有摩擦力的作用,摩擦力的方向水平向右 | |
| B. | 有摩擦力的作用,摩擦力的方向水平向左 | |
| C. | 有摩擦力的作用,但摩擦力的方向不能确定,因为m1、m2、θ1、θ2的数值并未给出 | |
| D. | 以上结论都不对 |
15.地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
| A. | 物体在赤道处受的地球引力等于两极处,而重力小于两极处 | |
| B. | 赤道处的角速度比北纬45°大 | |
| C. | 地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度比两极处大 | |
| D. | 地面上的物体随地球自转时提供向心力的是重力 |
12. 如图所示,一个重力为G的大砝码,用细线悬挂在O点,现在用力F拉法码,使悬线偏离竖直方向θ角时处于静止状态,此时所用拉力F的最小值为( )
如图所示,一个重力为G的大砝码,用细线悬挂在O点,现在用力F拉法码,使悬线偏离竖直方向θ角时处于静止状态,此时所用拉力F的最小值为( )
 如图所示,一个重力为G的大砝码,用细线悬挂在O点,现在用力F拉法码,使悬线偏离竖直方向θ角时处于静止状态,此时所用拉力F的最小值为( )
如图所示,一个重力为G的大砝码,用细线悬挂在O点,现在用力F拉法码,使悬线偏离竖直方向θ角时处于静止状态,此时所用拉力F的最小值为( )| A. | Gtanθ | B. | Gcosθ | C. | Gsinθ | D. | $\frac{G}{sinθ}$ |
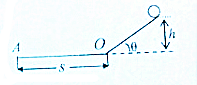 一光滑斜面圆滑地连接着一光滑平面,平面上的A点距斜面底端O为s,斜面倾角为θ如图,一小球从斜面上某处滑下要运动到A点所用时间最短,小球开始运动时所在的高度h为多少?最短时间是多少?
一光滑斜面圆滑地连接着一光滑平面,平面上的A点距斜面底端O为s,斜面倾角为θ如图,一小球从斜面上某处滑下要运动到A点所用时间最短,小球开始运动时所在的高度h为多少?最短时间是多少? 用两根轻质细线把两个质量未知的带电小球悬挂起来,a球带电+q,b球带电-2q,且两球间的库仑力小于b球受的重力,即两根线都处于竖直绷紧状态.若突然增加一个如图中所示的水平向左的匀强电场,待最后平衡时,表示平衡状态的图可能是( )
用两根轻质细线把两个质量未知的带电小球悬挂起来,a球带电+q,b球带电-2q,且两球间的库仑力小于b球受的重力,即两根线都处于竖直绷紧状态.若突然增加一个如图中所示的水平向左的匀强电场,待最后平衡时,表示平衡状态的图可能是( )


