题目内容
(2003年江苏)图中a所示为一根竖直悬挂的不可伸长的轻绳,下端拴一小物块A,上端固定在C点且与一能测量绳的拉力的测力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透).接着两者一起绕C点在竖直平面内做圆周运动.在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间t的变化关系如图中b所示.已知子弹射入的时间极短,且图中t=0为A、B开始以相同速度运动的时间,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?

解析:
解析:设A的质量为m,绳长为L,AB在最低点的速度为v1,在最高点的速度为v2,F1、F2分别表示绳子在最低点和最高点处的张力. 子弹射入A中,由动最守恒,m0v0=(m0+m)v1 ① AB在最低点时,F1-(m+m0)g=(m+m0) AB在最高点时,F2+(m+m0)g=(m+m0) AB从最低点到最高点机械能守恒, 2L(m+m0)g= 由图知,F1=Fm,F2=0,运动周期T=2t0. 联立上式,解得反映系统性质的物理量是:AB的运动周期T=2t0,A的质量m= AB一起运动的守恒量是机械能,选最低点为零势面,E= 将m、v1的值代入得 E= 答案:T=2t0、m= 机械能E= 归纳:这是一道探究性很强的开放性试题,体现了当前学习与考试的新特色.对于这类问题,首先依据情景联系我们熟悉的物理规律作出假设,然后尽可能全面、准确地列出反映规律的方程,再观察方程,看能求出哪些物理量.只要你敢假设,敢动手,一定会有收获.
|

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
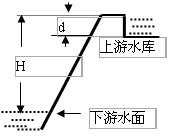
暑假作业北京艺术与科学电子出版社系列答案 (2006?江苏)我省沙河抽水蓄能电站自2003年投入运行以来,在缓解用电高峰电力紧张方面,取得了良好的社会效益和经济效益.抽蓄水能电站的工作原理是,在用电低谷时(如深夜),电站利用电网多余电能把水抽到高处蓄水池中,到用电高峰时,再利用蓄水池中的水发电.如图,蓄水池(上游水库)可视为长方体,有效总库容量(可用于发电)为V,蓄水后水位高出下游水面H,发电过程中上游水库水位最大落差为d.统计资料表明,该电站年抽水用电为2.4×108KW?h,年发电量为1.8×108KW?h.则下列计算结果正确的是(水的密度为ρ,重力加速度为g,涉及重力势能的计算均以下游水面为零势能面)( )
(2006?江苏)我省沙河抽水蓄能电站自2003年投入运行以来,在缓解用电高峰电力紧张方面,取得了良好的社会效益和经济效益.抽蓄水能电站的工作原理是,在用电低谷时(如深夜),电站利用电网多余电能把水抽到高处蓄水池中,到用电高峰时,再利用蓄水池中的水发电.如图,蓄水池(上游水库)可视为长方体,有效总库容量(可用于发电)为V,蓄水后水位高出下游水面H,发电过程中上游水库水位最大落差为d.统计资料表明,该电站年抽水用电为2.4×108KW?h,年发电量为1.8×108KW?h.则下列计算结果正确的是(水的密度为ρ,重力加速度为g,涉及重力势能的计算均以下游水面为零势能面)( )