Question

半径为R的大圆盘以角速度ω旋转，如图所示，有人站在盘边的P点上随盘转动，他想用枪击中盘中心的目标O，若子弹离开枪口的速度为V，不计空气阻力，则（ ）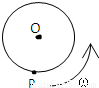

A．枪应向PO的左方偏过θ角射击，而sinθ=ωR/V
B．枪应瞄准目标O射击
C．枪应向PO的右方偏过θ角射击，而cosθ=ωR/V
D．枪应向PO的左方偏过θ角射击，而tanθ=ωR/V

Answer 1

【答案】分析：子弹参与了两个方向上的运动，沿枪口方向上的运动和沿圆盘切线方向上的运动，当合速度的方向指向目标O时，击中目标．根据平行四边形定则进行分析．
解答：解：子弹沿圆盘切线方向上的速度v₁=Rω，子弹沿枪口方向上的速度为v_o，
根据平行四边形定则，有sinθ==．
所以v的方向应瞄准PO的左方偏过θ角射击，且sin θ=．故A正确，B、C、D错误．
故选A．
点评：解决本题的关键知道子弹参与两个分运动，抓住合速度的方向指向O点，运用平行四边形定则求解．