题目内容
 如图,水平地面上有一楔形物块a,倾角为θ=37°,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a与b以共同速度在地面轨道的光滑段向左匀速运动.当它们刚运行至轨道的粗糙段时(物块a与粗糙地面的动摩擦因数为μ,g=10m/s2),( )
如图,水平地面上有一楔形物块a,倾角为θ=37°,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a与b以共同速度在地面轨道的光滑段向左匀速运动.当它们刚运行至轨道的粗糙段时(物块a与粗糙地面的动摩擦因数为μ,g=10m/s2),( )分析:本题应分匀速运动和减速运动两个过程分别对两个物体受力分析,根据共点力平衡条件和牛顿第二定律列式求解.用临界条件来判定ab的相对运动情况,进而确定答案.
解答:解:
在光滑段运动时,物块a及物块b均处于平衡状态,对a、b整体受力分析,受重力和支持力,二力平衡;

对b受力分析,如上图,受重力、支持力、绳子的拉力,根据共点力平衡条件,有
Fcosθ-F Nsinθ=0 ①;
Fsinθ+F Ncosθ-mg=0 ②;
由①②两式解得:F=mgsinθ,FN=mgcosθ;
当它们刚运行至轨道的粗糙段时,减速滑行,系统有水平向右的加速度,若μ=0.75时,a向右的加速度大小为:a0=μg=0.75×10m/s2=7.5m/s2.
而b向右的加速度最大为:am=gtanθ=10×
m/s2=7.5m/s2,此时绳对b没有拉力.
故可知:
AB、若μ=0.1,则物块a、b仍相对静止,竖直方向加速度为零,由牛顿第二定律得到:
Fsinθ+F Ncosθ-mg=0 ③;
F Nsinθ-Fcosθ=ma ④;
由③④两式解得:F=mgsinθ-macosθ,FN=mgcosθ+masinθ;
即绳的张力F将减小,而a对b的支持力变大;
再对a、b整体受力分析竖直方向重力和支持力平衡,水平方向只受摩擦力,重力和支持力二力平衡,故地面对a支持力不变.
故A错误,B正确.
CD、若μ=0.75,a的加速度为7.5m/s2,物块b的重力和支持力正好提供其运动的加速度,故绳的拉力为零,FN=mgcosθ+masinθ;斜面对b的支持力也增大.
故C错误,D正确.
故选:BD
在光滑段运动时,物块a及物块b均处于平衡状态,对a、b整体受力分析,受重力和支持力,二力平衡;

对b受力分析,如上图,受重力、支持力、绳子的拉力,根据共点力平衡条件,有
Fcosθ-F Nsinθ=0 ①;
Fsinθ+F Ncosθ-mg=0 ②;
由①②两式解得:F=mgsinθ,FN=mgcosθ;
当它们刚运行至轨道的粗糙段时,减速滑行,系统有水平向右的加速度,若μ=0.75时,a向右的加速度大小为:a0=μg=0.75×10m/s2=7.5m/s2.
而b向右的加速度最大为:am=gtanθ=10×
| 3 |
| 4 |
故可知:
AB、若μ=0.1,则物块a、b仍相对静止,竖直方向加速度为零,由牛顿第二定律得到:
Fsinθ+F Ncosθ-mg=0 ③;
F Nsinθ-Fcosθ=ma ④;
由③④两式解得:F=mgsinθ-macosθ,FN=mgcosθ+masinθ;
即绳的张力F将减小,而a对b的支持力变大;
再对a、b整体受力分析竖直方向重力和支持力平衡,水平方向只受摩擦力,重力和支持力二力平衡,故地面对a支持力不变.
故A错误,B正确.
CD、若μ=0.75,a的加速度为7.5m/s2,物块b的重力和支持力正好提供其运动的加速度,故绳的拉力为零,FN=mgcosθ+masinθ;斜面对b的支持力也增大.
故C错误,D正确.
故选:BD
点评:本题关键要熟练运用整体法和隔离法对物体受力,另外要用特殊值来判定,同时要能结合牛顿运动定律求解!解综合能力要求较高.

练习册系列答案
相关题目
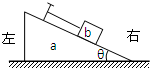 如图,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时,关于b之后的运动情况和地面对a的支持力,下列说法中正确的是( )
如图,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时,关于b之后的运动情况和地面对a的支持力,下列说法中正确的是( )| A、b将一定沿a的斜面上滑,地面对a的支持力减小 | B、b可能相对a的斜面静止,地面对a的支持力不变 | C、b将一定沿a的斜面上滑,地面对a的支持力增大 | D、绳的张力一定减小,b一定相对a的斜面静止,地面对a的支持力不变 |
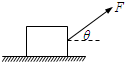 如图,水平地面上有一木箱,木箱与地面间的动摩擦因数为μ,木箱在与水平夹角为θ的拉力F作用下做匀速直线运动.在θ从0逐渐增大到90°的过程中,木箱的速度始终保持不变,则拉力F的功率( )
如图,水平地面上有一木箱,木箱与地面间的动摩擦因数为μ,木箱在与水平夹角为θ的拉力F作用下做匀速直线运动.在θ从0逐渐增大到90°的过程中,木箱的速度始终保持不变,则拉力F的功率( )| A、一直增大 | B、一直减小 | C、先减小后增大 | D、先增大后减小 |
 (2008?海南)如图,水平地面上有一楔形物体b,b的斜面上有一小物块a;a与b之间、b与地面之间均存在摩擦.已知楔形物体b静止时,a静止在b的斜面上.现给a和b一个共同的向左的初速度,与a和b都静止时相比,此时可能( )
(2008?海南)如图,水平地面上有一楔形物体b,b的斜面上有一小物块a;a与b之间、b与地面之间均存在摩擦.已知楔形物体b静止时,a静止在b的斜面上.现给a和b一个共同的向左的初速度,与a和b都静止时相比,此时可能( )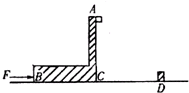 如图,水平地面上有一“L”型滑板ACB,A到地面的竖直高度为h=1.8m.水
如图,水平地面上有一“L”型滑板ACB,A到地面的竖直高度为h=1.8m.水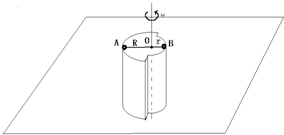 m/s2,求:
m/s2,求: