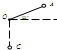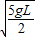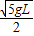Question

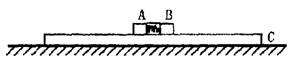
长为L的细线，拴一质量为m的小球，一端固定于O点.让其在水平面内做匀速圆周运动(这种运动通常称为圆锥摆运动)，如图6-7-10所示.当摆线L与竖直方向的夹角是α时，求：

图6-7-10

(1)线的拉力F；

(2)小球运动的线速度的大小；

(3)小球运动的角速度及周期.

Answer 1

解析：首先明确物体的运动情况：匀速圆周运动，此时提供的向心力等于物体圆周运动所需要的向心力，由此可以建立等式列出方程.这就要求对物体进行受力分析，找出沿半径方向的合力，即向心力，而需要的向心力表达式直接由公式得出，这样问题就迎刃而解.

    做匀速圆周运动的小球受力如右图所示，小球受重力mg和绳子的拉力F.

    因为小球在水平面内做匀速圆周运动，所以小球受到的合力指向圆心O′，且是水平方向.

由平行四边形定则得小球受到的合力大小为mgtanα,线对小球的拉力大小为：F=mg/cosα.

    由牛顿第二定律得：mgtanα=

    由几何关系得r=Lsinα

    所以,小球做匀速圆周运动线速度的大小为

v=

    小球运动的角速度

ω=

    小球运动的周期T=.

答案：（1）F=mg/cosα  （2）v=（3）ω=      T=