题目内容
如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出:(1)小球到达轨道最高点时的速度为多大?
(2)小球落地时距离A点多远?落地时速度多大?
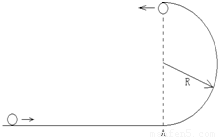
【答案】分析:(1)根据最高点轨道对球的弹力,运用牛顿第二定律求出小球在最高点的速度大小.
(2)小球离开最高点最平抛运动,根据高度求出运动的时间,从而根据水平方向上的运动求出小球落地点距离A点的距离.根据运动学公式求出落地时水平方向和竖直方向的速度,根据平行四边形定则求出落地的速度大小.
解答:解:(1)根据牛顿第三定律,小球到达轨道的最高点时受到轨道的支持力N等于小球对轨道的压力N‘,则:N=mg,
由题意可知小球在最高点时,有: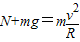 ,
,
解得小球到达轨道最高点时的速度大小为: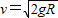
(2)小球离开轨道平面做平抛运动: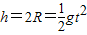 ,
,
即平抛运动时间: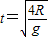 ,
,
所以小球落地时与A点的距离: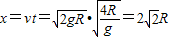
落地时竖直方向分速度vy,有: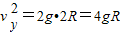
落地时水平方向分速度vx,有: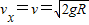
所以小球落地时速度大小为: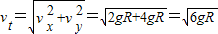 .
.
答:(1)小球到达轨道最高点时的速度为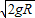 .
.
(2)小球落地时距离A点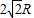 ,落地时速度为
,落地时速度为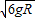 .
.
点评:本题考查了圆周运动和平抛运动的基本知识,关键掌握平抛运动在水平方向和竖直方向上的运动规律以及圆周运动的向心力来源.
(2)小球离开最高点最平抛运动,根据高度求出运动的时间,从而根据水平方向上的运动求出小球落地点距离A点的距离.根据运动学公式求出落地时水平方向和竖直方向的速度,根据平行四边形定则求出落地的速度大小.
解答:解:(1)根据牛顿第三定律,小球到达轨道的最高点时受到轨道的支持力N等于小球对轨道的压力N‘,则:N=mg,
由题意可知小球在最高点时,有:
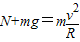 ,
,解得小球到达轨道最高点时的速度大小为:
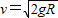
(2)小球离开轨道平面做平抛运动:
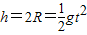 ,
,即平抛运动时间:
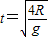 ,
,所以小球落地时与A点的距离:
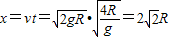
落地时竖直方向分速度vy,有:
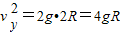
落地时水平方向分速度vx,有:
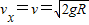
所以小球落地时速度大小为:
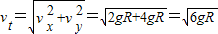 .
.答:(1)小球到达轨道最高点时的速度为
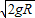 .
.(2)小球落地时距离A点
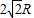 ,落地时速度为
,落地时速度为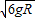 .
.点评:本题考查了圆周运动和平抛运动的基本知识,关键掌握平抛运动在水平方向和竖直方向上的运动规律以及圆周运动的向心力来源.

练习册系列答案
相关题目
 如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,轨道半径为R,小球在轨道的最高点对轨道的压力等于小球的重力.求:
如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,轨道半径为R,小球在轨道的最高点对轨道的压力等于小球的重力.求: 如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,轨道半径为R,小球在轨道的最高点对轨道的压力等于小球的重力.则( )
如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,轨道半径为R,小球在轨道的最高点对轨道的压力等于小球的重力.则( ) 如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出:
如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出: 如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出:
如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出: