题目内容
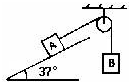
如图所示,斜面与水平面间的夹角![]() ,物体A和B的质量分别为
,物体A和B的质量分别为![]() 、
、![]() 。两者之间用质量可以不计的细绳相连。求:
。两者之间用质量可以不计的细绳相连。求:
(1)如A和B对斜面的动摩擦因数分别为![]() ,
,![]() 时,两物体的加速度各为多大?绳的张力为多少?
时,两物体的加速度各为多大?绳的张力为多少?
(2)如果把A和B位置互换,两个物体的加速度及绳的张力各是多少?
(3)如果斜面为光滑时,则两个物体的加速度及绳的张力又各是多少?

(1)A静止 aB=3.27m/s2
(2)![]() ,
,![]()
(3)加速度均为![]() ,两物间无作用力。
,两物间无作用力。
解析:
(1)设绳子的张力为![]() ,物体A和B沿斜面下滑的加速度分别为
,物体A和B沿斜面下滑的加速度分别为![]() 和
和![]() ,根据牛顿第二定律:
,根据牛顿第二定律:
对A有![]()
对B有![]()
设![]() ,即假设绳子没有张力,联立求解得
,即假设绳子没有张力,联立求解得![]() ,因
,因![]() ,故
,故![]()
说明物体B运动比物体A的运动快,绳松弛,所以![]() 的假设成立。故有
的假设成立。故有![]() 因而实际不符,则A静止。
因而实际不符,则A静止。![]()
(2)如B与A互换则![]() ,即B物运动得比A物快,所以A、B之间有拉力且共速,用整体法
,即B物运动得比A物快,所以A、B之间有拉力且共速,用整体法
![]()
代入数据求出![]() ,用隔离法对B:
,用隔离法对B:![]() 代入数据求出
代入数据求出![]()
(3)如斜面光滑摩擦不计,则A和B沿斜面的加速度均为![]() 两物间无作用力。
两物间无作用力。

练习册系列答案
相关题目
 如图所示,斜面与水平面的夹角为37°,物体A质量为2kg,与斜面间摩擦因数为0.4,求:
如图所示,斜面与水平面的夹角为37°,物体A质量为2kg,与斜面间摩擦因数为0.4,求: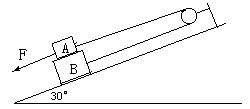 如图所示,斜面与水平方向成
如图所示,斜面与水平方向成