题目内容
 (2012?徐州一模)某同学设计了一个探究加速度a与物体所受合力 F及质量m关系的实验,图(a)为实验装置简图.(交流电的频率为50Hz)
(2012?徐州一模)某同学设计了一个探究加速度a与物体所受合力 F及质量m关系的实验,图(a)为实验装置简图.(交流电的频率为50Hz)(1)图(b)为某次实验得到的纸带,根据纸带可求出小车的加速度大小为
3.2
3.2
m/s2.(保留二位有效数字)(2)保持砂和砂桶质量不变,改变小车质量m,分别得到小车加速度a与质量m及对应的1/m,数据如下表:

| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 小车加速度a/m?s-2 | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 | ||
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 | ||
|
4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
a=
| 1 |
| 2m |
a=
.| 1 |
| 2m |
(3)有一位同学通过实验测量作出了图(c)中的A图线,另一位同学实验测出了如图(c)中的B图线.试分析
①A图线不通过坐标原点的原因是
没有平衡摩擦力或平衡摩擦力不够
没有平衡摩擦力或平衡摩擦力不够
;②A图线上部弯曲的原因是
随F的增加不再满足沙和沙桶的质量远小于小车的质量
随F的增加不再满足沙和沙桶的质量远小于小车的质量
;③B图线在纵轴上有截距的原因是
平衡摩擦力时,长木板倾角过大(平衡摩擦力过度)
平衡摩擦力时,长木板倾角过大(平衡摩擦力过度)
.分析:(1)利用逐差法△s=aT2求解物体的加速度;
(2)由图表所给的数据通过描点连线得出物体的加速度a和物体质量的倒数
之间的关系.
(3)①根据只有当F增大到一定值时物体才开始具有加速度,得出没有平衡摩擦力或摩擦力平衡不够.
②根据牛顿第二定律求出系统的加速度,最终求出绳子的拉力和沙和沙桶的重力之间的关系得出只有m<<M时,才有F≈mg,才有物体的加速度正比于物体所受的合外力.得出图象弯曲的原因是:未满足沙和沙桶质量远小于小车的质量.
③在拉力F=0时物体的加速度不为0,故有mgsinθ-μmgcosθ=ma,得出tanθ>μ.即在平衡摩擦力时,长木板倾角过大(平衡摩擦力过度).
(2)由图表所给的数据通过描点连线得出物体的加速度a和物体质量的倒数
| 1 |
| m |
(3)①根据只有当F增大到一定值时物体才开始具有加速度,得出没有平衡摩擦力或摩擦力平衡不够.
②根据牛顿第二定律求出系统的加速度,最终求出绳子的拉力和沙和沙桶的重力之间的关系得出只有m<<M时,才有F≈mg,才有物体的加速度正比于物体所受的合外力.得出图象弯曲的原因是:未满足沙和沙桶质量远小于小车的质量.
③在拉力F=0时物体的加速度不为0,故有mgsinθ-μmgcosθ=ma,得出tanθ>μ.即在平衡摩擦力时,长木板倾角过大(平衡摩擦力过度).
解答:解: (1)任意两个计数点之间的时间间隔
(1)任意两个计数点之间的时间间隔
t=2T=
=
=0.04s
根据逐差法△s=aT2可得物体的加速度
a=
=
=3.2m/s2
(2)由图表分析可知物体加速度a的2倍等于物体质量的倒数即a=
.
根据图表在坐标纸上描点,然后用一条直线将这些点和坐标原点连接起来,图象如图所示.
(3)①A图线中当F≠0时物体的加速度a=0,即只有当F增大到一定值时物体才开始具有加速度,故在物体保持静止的时候其所受的静摩擦力等于绳子的拉力,所以出现此现象的原因是没有平衡摩擦力或摩擦力平衡不够.
②设物体的加速度为a,绳子拉力为F,以沙和沙桶为研究对象mg-F=ma
以小车为研究对象F=Ma
解得a=
故F=Ma=M
=
mg
要物体M的加速度a正比于物体所受的合外力mg.
则
为常数,即不随m的增大而变化,故有m+M≈M,所以必有m《M,而不满足m《M时,随m的增大物体的加速度a逐渐减小.故图象弯曲的原因是:未满足沙和沙桶质量远小于小车的质量.
③从B图可知在拉力F=0时物体的加速度不为0,即合外力不为0,则mgsinθ-μmgcosθ=ma,由于a>0,故mgsinθ-mgcosθ>0,故有mgsin>μmgcosθ,得sinθ>μcosθ,即tanθ>μ.
B图纵轴的截距大于0,说明在无拉力的情况下物体的加速度大于0,即在平衡摩擦力时,长木板倾角过大(平衡摩擦力过度).
故本题的答案为:(1)3.2;
(2)a=
;
(3)①没有平衡摩擦力或摩擦力平衡不够;
②未满足沙和沙桶质量远小于小车的质量;
③在平衡摩擦力时,长木板倾角过大(平衡摩擦力过度).
 (1)任意两个计数点之间的时间间隔
(1)任意两个计数点之间的时间间隔t=2T=
| 2 |
| f |
| 2 |
| 50 |
根据逐差法△s=aT2可得物体的加速度
a=
| X3+X4-X1- X2 |
| 4(2T)2 |
| 7.72+7.21-6.70-6.19 |
| 4×(0.04)2 |
=3.2m/s2
(2)由图表分析可知物体加速度a的2倍等于物体质量的倒数即a=
| 1 |
| 2m |
根据图表在坐标纸上描点,然后用一条直线将这些点和坐标原点连接起来,图象如图所示.
(3)①A图线中当F≠0时物体的加速度a=0,即只有当F增大到一定值时物体才开始具有加速度,故在物体保持静止的时候其所受的静摩擦力等于绳子的拉力,所以出现此现象的原因是没有平衡摩擦力或摩擦力平衡不够.
②设物体的加速度为a,绳子拉力为F,以沙和沙桶为研究对象mg-F=ma
以小车为研究对象F=Ma
解得a=
| mg |
| M+m |
故F=Ma=M
| mg |
| M+m |
| M |
| m+M |
要物体M的加速度a正比于物体所受的合外力mg.
则
| M |
| m+M |
③从B图可知在拉力F=0时物体的加速度不为0,即合外力不为0,则mgsinθ-μmgcosθ=ma,由于a>0,故mgsinθ-mgcosθ>0,故有mgsin>μmgcosθ,得sinθ>μcosθ,即tanθ>μ.
B图纵轴的截距大于0,说明在无拉力的情况下物体的加速度大于0,即在平衡摩擦力时,长木板倾角过大(平衡摩擦力过度).
故本题的答案为:(1)3.2;
(2)a=
| 1 |
| 2m |
(3)①没有平衡摩擦力或摩擦力平衡不够;
②未满足沙和沙桶质量远小于小车的质量;
③在平衡摩擦力时,长木板倾角过大(平衡摩擦力过度).
点评:根据实验原理求出绳子的拉力和加速度之间的关系,加速度和沙与沙桶的重力之间的关系,加速度和摩擦因数之间的关系是解决本题的关键所在.

练习册系列答案
相关题目
 (2012?徐州一模)如图所示,在真空中有两个带正电的点电荷,分别置于P、Q两点,P处正点电荷的电荷量大于Q处点电荷的电荷量,A、B为P、Q连线的中垂线上的两点,现将一负电荷q 由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
(2012?徐州一模)如图所示,在真空中有两个带正电的点电荷,分别置于P、Q两点,P处正点电荷的电荷量大于Q处点电荷的电荷量,A、B为P、Q连线的中垂线上的两点,现将一负电荷q 由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
 (2012?徐州一模)如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处.(g=10m/s2)求:
(2012?徐州一模)如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC,其下端(C端)距地面高度h=0.8m.有一质量500g的带电小环套在直杆上,正以某一速度沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处.(g=10m/s2)求: (2012?徐州一模)如图所示,三根通电长直导线P、Q、R互相平行,垂直纸面放置,其间距均为a,电流强度均为I,方向垂直纸面向里(已知电流为I的长直导线产生的磁场中,距导线r处的磁感应强度B=kI/r,其中k为常数).某时刻有一电子(质量为m、电量为e)正好经过原点O,速度大小为v,方向沿y轴正方向,则电子此时所受磁场力为( )
(2012?徐州一模)如图所示,三根通电长直导线P、Q、R互相平行,垂直纸面放置,其间距均为a,电流强度均为I,方向垂直纸面向里(已知电流为I的长直导线产生的磁场中,距导线r处的磁感应强度B=kI/r,其中k为常数).某时刻有一电子(质量为m、电量为e)正好经过原点O,速度大小为v,方向沿y轴正方向,则电子此时所受磁场力为( )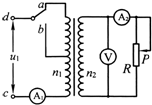 (2012?徐州一模)如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,除R以外其余电阻不计.从某时刻开始在原线圈c、d两端加上
(2012?徐州一模)如图所示,理想变压器原、副线圈的匝数比为10:1,b是原线圈的中心抽头,电压表和电流表均为理想电表,除R以外其余电阻不计.从某时刻开始在原线圈c、d两端加上