题目内容
(18分)在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示。第一象限内有竖直向上的匀强电场,第二象限内有一水平向右的匀强电场。某种发射装置(未画出)竖直向上发射出一个质量为m、电荷量为q的带正电粒子(可视为质点),该粒子以v0的初速度从x轴上的A点进入第二象限,并从y轴上的C点沿水平方向进入第一象限后能够沿水平方向运动到D点。已知OA、OC距离相等,CD的距离为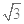 OC,E点在D点正下方,位于x轴上,重力加速度为g。则:
OC,E点在D点正下方,位于x轴上,重力加速度为g。则:

(1)求粒子在C点的速度大小以及OC之间的距离;
(2)若第一象限同时存在按如图乙所示规律变化的磁场,磁场方向垂直纸面,(以垂直纸面向外的磁场方向为正方向,图中B0,T0均为未知量),并且在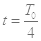 时刻粒子由C点进入第一象限,且恰好也能通过同一水平线上的D点,速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同,求交变磁场变化的周期;
时刻粒子由C点进入第一象限,且恰好也能通过同一水平线上的D点,速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同,求交变磁场变化的周期;
(3)若第一象限仍同时存在按如图乙所示规律变化的磁场(以垂直纸面向外的磁场方向为正方向,图中B0,T0均为未知量),调整图乙中磁场变化的周期,让粒子在t=0时刻由C点进入第一象限,且恰能通过E点,求交变磁场的磁感应强度B0应满足的条件。
(1)
 (2)
(2) (3)
(3)
【解析】
试题分析:(1)粒子抛出后,竖直方向受重力作用,匀减速直线运动,加速度 ,到达C点时只有水平速度,竖直速度等于0,因此有
,到达C点时只有水平速度,竖直速度等于0,因此有
,水平方向受到电场力作用为初速度0的匀加速直线运动,
整理得 即粒子在C点的速度大小为
即粒子在C点的速度大小为
对竖直方向的匀减速直线运动有
解得
(2)在第一象限没有磁场存在时,粒子能沿水平线运动,说明
加上磁场后粒子将在洛伦兹力作用下做匀速圆周运动,
由于磁场周期性变化,所以粒子运动轨迹也是周期性变化, 时刻进入磁场开始圆周运动,要回到同一水平线上的D点,运动轨迹如下图所示
时刻进入磁场开始圆周运动,要回到同一水平线上的D点,运动轨迹如下图所示

洛伦兹力提供向心力 ,CD的长度
,CD的长度 
根据几何关系
即得磁感应强度
粒子做圆周运动的周期
有运动轨迹判断磁场变化的周期
(3)粒子在t=0时刻由C点进入第一象限,且恰能通过E点,运动轨迹如下图所示。有几何关系得

则每经过磁场的半个周期,粒子转过 的圆心角,对应的弦长刚好等于圆周运动的半径R。
的圆心角,对应的弦长刚好等于圆周运动的半径R。


洛伦兹力提供向心力
整理得
考点:带电粒子在复合场中的运动

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案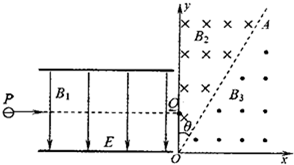 如图所示,水平放置的两平行金属板间存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度为B1,方向与纸面垂直,电场的场强E=2.0×105V/m,方向竖直向下,PQ为板间中线.紧靠平行板右侧边缘建立平面直角坐标系xOy,在第一象限内,存在着以AO为理想边界的两个匀强磁场区域,方向如图所示,磁感应强度B2=B3=0.6T,AO和y轴间的夹角θ=30°.一束带负电的粒子,质量不同,带电量q=2.5×10-8C,以v=5×105m/s的水平速度从P点射入板间,沿PQ做直线运动,穿出平行板区域后从y轴上坐标为(0,0.3m)的Q点垂直于y轴射入磁场区域.(粒子的重力不计)
如图所示,水平放置的两平行金属板间存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度为B1,方向与纸面垂直,电场的场强E=2.0×105V/m,方向竖直向下,PQ为板间中线.紧靠平行板右侧边缘建立平面直角坐标系xOy,在第一象限内,存在着以AO为理想边界的两个匀强磁场区域,方向如图所示,磁感应强度B2=B3=0.6T,AO和y轴间的夹角θ=30°.一束带负电的粒子,质量不同,带电量q=2.5×10-8C,以v=5×105m/s的水平速度从P点射入板间,沿PQ做直线运动,穿出平行板区域后从y轴上坐标为(0,0.3m)的Q点垂直于y轴射入磁场区域.(粒子的重力不计)


 如下图所示,两平行金属板间存在相互平行的匀强磁场和匀强电场,电场强度为E,磁感强度为B,方向都在竖直平面内与金属板相垂直.平行板右侧有一荧光屏MN在竖直平面内与金属板相垂直.荧光屏MN中心为O,O'是电、磁场上边缘的一点,连线OO'垂直荧光屏MN,其长度为L,在荧光屏MN上建立一直角坐标系,原点为O,y轴向上,x轴垂直纸面向外,一束具有相同速度和荷质比的带电粒子,沿OO'方向由O射入此电、磁场中,最后打在荧光屏上,屏上亮点坐标为
如下图所示,两平行金属板间存在相互平行的匀强磁场和匀强电场,电场强度为E,磁感强度为B,方向都在竖直平面内与金属板相垂直.平行板右侧有一荧光屏MN在竖直平面内与金属板相垂直.荧光屏MN中心为O,O'是电、磁场上边缘的一点,连线OO'垂直荧光屏MN,其长度为L,在荧光屏MN上建立一直角坐标系,原点为O,y轴向上,x轴垂直纸面向外,一束具有相同速度和荷质比的带电粒子,沿OO'方向由O射入此电、磁场中,最后打在荧光屏上,屏上亮点坐标为