题目内容
质量为40kg的雪橇在倾角θ=37°的斜面上向下滑动（如图甲所示），所受的空气阻力与速度成正比．今测得雪橇运动的v-t图象如图乙所示，且AB是曲线的切线，B点坐标为（4，15），CD是曲线的渐近线．试求空气的阻力系数k和雪橇与斜坡间的动摩擦因数μ．
分析：AB是曲线的切线的斜率表示速度为5m/s时的加速度大小，根据牛顿第二定律列出速度是5m/s时、以及加速度为零时的动力学方程．联立两方程求出空气的阻力系数k和雪橇与斜坡间的动摩擦因数μ．
解答：解：由牛顿运动定律得mgsin θ-μFN-kv=ma
由平衡条件得FN=mgcos θ
由图象得A点，vA=5 m/s，加速度aA=2.5 m/s2；
有：mgsin θ-μFN-kvA=maA．①
最终雪橇匀速运动时最大速度vm=10 m/s，a=0
mgsin θ-μFN-kvm=0②
联立①②，代入数据解得μ=0.125，k=20 kg/s．
答：出空气的阻力系数k为20kg/s，雪橇与斜坡间的动摩擦因数μ为0.125．
由平衡条件得FN=mgcos θ
由图象得A点，vA=5 m/s，加速度aA=2.5 m/s2；
有：mgsin θ-μFN-kvA=maA．①
最终雪橇匀速运动时最大速度vm=10 m/s，a=0
mgsin θ-μFN-kvm=0②
联立①②，代入数据解得μ=0.125，k=20 kg/s．
答：出空气的阻力系数k为20kg/s，雪橇与斜坡间的动摩擦因数μ为0.125．
点评：本题考查了学生的看图分析图象的能力，能根据图象从中找出有用的信息，结合牛顿第二定律进行求解．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
如图所示，质量为40kg的雪橇（包括人）在与水平方向成37°角、大小为200N的拉力F作用下，沿水平面由静止开始运动，雪橇与地面间动摩擦因数为0.2（取g=10m/s2，cos37°=0.8，sin37°=0.6 ）求：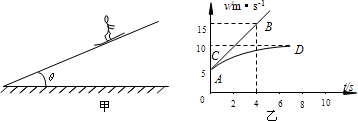
质量为40kg的雪橇在倾角θ=37°的斜面上向下滑动如图甲所示，所受的空气阻力与速度成正比．今测得雪橇运动的v-t图象如图乙所示，且AB是曲线的切线，B点坐标为（4，15），CD是曲线的渐近线，g取10m/s2．根据以上信息，不可以确定下列哪个物理量（ ）
如图所示，质量为40kg的雪橇（包括人）在与水平方向成37°角、大小为200N的拉力F作用下，沿水平面由静止开始运动，经过2s撤去拉力F，雪橇与地面间动摩擦因数为0.20．取g=10m/s2，cos37°=0.8，sin37°=0.6．求：
=370 的斜面上向下滑动，如图（a）所示，所受的空气阻力与速度成正比，今测得雪橇运动的v-t图象如（b）所示，且AB是曲线在A点切线，B点坐标为（4，15），CD是曲线的渐近线。根据以上信息，不可以确定下列哪个物理量（ ）