题目内容
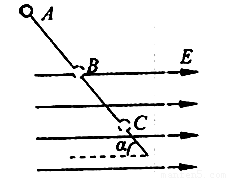
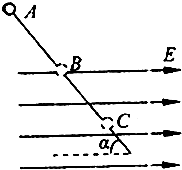 一根光滑的绝缘细杆与水平成a=30°倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为l=1m,如图,求:(g取10m/s2)
一根光滑的绝缘细杆与水平成a=30°倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为l=1m,如图,求:(g取10m/s2)(1)小球进入电场后还能滑行多远?
(2)小球从A滑至最远时间是多少?
分析:(1)对于整个过程,运用动能定理列式,即可求得小球进入电场后滑行的距离.
(2)根据动能定理研究AB段,求出小球经过B点的速度.由位移与平均速度的关系,列式求解两段过程的时间,得到总时间.
(2)根据动能定理研究AB段,求出小球经过B点的速度.由位移与平均速度的关系,列式求解两段过程的时间,得到总时间.
解答:解:(1)设小球进入电场后还能滑行距离为s,滑行到C点速度为零.
对于小球的整个滑行过程,由动能定理得:
mg(l+s)sinα-qEscosα=0
则得 s=
l=
×1m=1m.
(2)设小球经过B点的速度为v.
对于小球从A到B的过程,由动能定理得:
mglsinα=
mv2
则得 v=
=
m/s=
m/s
根据运动学公式得:l+s=
tAB+
tBC,
而总时间 t=tAB+tBC,
联立得 t=
=
s=1.26s
答:
(1)小球进入电场后还能滑行1m.
(2)小球从A滑至最远时间是1.26s.
对于小球的整个滑行过程,由动能定理得:
mg(l+s)sinα-qEscosα=0
则得 s=
| mgsinα |
| qEcosα-mgsinα |
| 3×10-2×10×0.5 | ||||
1.73×10-5×2×104×
|
(2)设小球经过B点的速度为v.
对于小球从A到B的过程,由动能定理得:
mglsinα=
| 1 |
| 2 |
则得 v=
| 2glsinα |
| 2×10×1×0.5 |
| 10 |
根据运动学公式得:l+s=
| v |
| 2 |
| v |
| 2 |
而总时间 t=tAB+tBC,
联立得 t=
| 2(l+s) |
| v |
| 2×(1+1) | ||
|
答:
(1)小球进入电场后还能滑行1m.
(2)小球从A滑至最远时间是1.26s.
点评:本题涉及力在空间的效果,运用动能定理求解距离比较简单方便,运用平均速度求时间比较简便.也可以根据牛顿第二定律和运动学公式结合求解.

练习册系列答案
相关题目
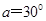 倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为
倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为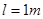 ,如图,求:
,如图,求: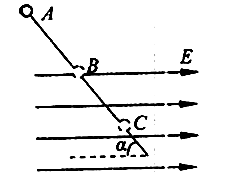
 倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为
倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为 ,如图,求:
,如图,求: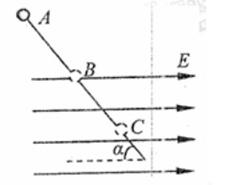
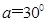 倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为
倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为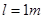 ,如图,求:
,如图,求: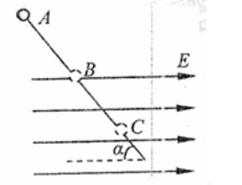
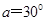 倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为
倾斜放置,其BC部分在向右的匀强电场中,电场强度E=2×104N/C,在细杆上套一个带负电的电量q=1.73×10-5C,质量m=3×10-2kg的小球,今使小球由A点静止沿杆下滑从B点进入电场,已知AB长为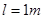 ,如图,求:
,如图,求: