题目内容
如图所示,两段长均为L的轻质线共同系住一个质量为m的小球,另一端分别固定在等高的A,B两点,A,B两点间距也为L,今使小球在竖直平面内做圆周运动,当小球到达最高点的速率为v时,两段线中张力恰好均为零,若小球到达最高点速率为2v。则此时每段线中张力为多少?(重力加速度为g)

解析试题分析:当小球到达最高点速率为v时,有 当小球到达最高点速率为2v时,应有
当小球到达最高点速率为2v时,应有 ,所以,此时最高点各力如图所示,所以
,所以,此时最高点各力如图所示,所以 .
.
考点:牛顿第二定律;向心力.

练习册系列答案
相关题目
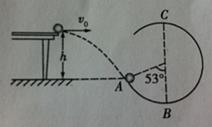
质量为 、长为L=5 m的木板放在水平面上,木板与水平面的动摩擦因数为
、长为L=5 m的木板放在水平面上,木板与水平面的动摩擦因数为 .将质量m=10 kg的小木块(可视为质点),以
.将质量m=10 kg的小木块(可视为质点),以 的速度从木板的左端水平抛射到木板上(如图所示),小木块与木板面的动摩擦因数为
的速度从木板的左端水平抛射到木板上(如图所示),小木块与木板面的动摩擦因数为 (最大静摩擦力等于滑动摩擦力,
(最大静摩擦力等于滑动摩擦力, ).则以下判断中正确的是( )
).则以下判断中正确的是( )
| A.木板一定静止不动,小木块不能滑出木板 |
| B.木板一定静止不动,小木块能滑出木板 |
| C.木板一定向右滑动,小木块不能滑出木板 |
| D.木板一定向右滑动,小木块能滑出木板 |
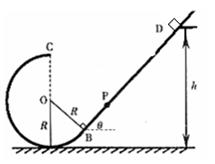
 ,不计一切摩擦和阻力。求:
,不计一切摩擦和阻力。求:

 由
由 板左端靠近板面的位置,沿垂直于磁场且平行于板面的方向射入磁场区。当
板左端靠近板面的位置,沿垂直于磁场且平行于板面的方向射入磁场区。当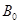 和
和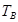 取某些特定值时,可使
取某些特定值时,可使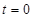 时刻入射的粒子经
时刻入射的粒子经 时间恰能垂直打在
时间恰能垂直打在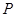 板上(不考虑粒子反弹)。上述
板上(不考虑粒子反弹)。上述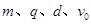 为已知量。
为已知量。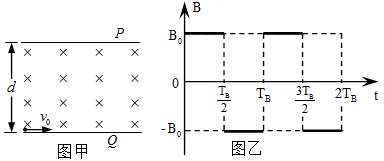
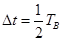 ,求
,求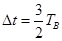 ,求粒子在磁场中运动时加速度的大小;
,求粒子在磁场中运动时加速度的大小; 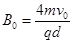 ,为使粒子仍能垂直打在
,为使粒子仍能垂直打在