题目内容
20. 如图所示,每米电阻为1Ω的一段导线被弯成半径为r=1m的三段圆弧,并组成闭合回路.每段圆弧都是四分之一圆周,位于空间直角坐标系的不同平面内,其中ab段位于xOy平面内,bc段位于yOz平面内,ca段位于zOx平面内.空间存在一个沿+x轴方向的磁场,其磁感应强度大小随时间变化的关系式为B=0.7+0.6t,则导线中的感应电流方向是a→c→b→a(用字母表示),大小是0.1A.
如图所示,每米电阻为1Ω的一段导线被弯成半径为r=1m的三段圆弧,并组成闭合回路.每段圆弧都是四分之一圆周,位于空间直角坐标系的不同平面内,其中ab段位于xOy平面内,bc段位于yOz平面内,ca段位于zOx平面内.空间存在一个沿+x轴方向的磁场,其磁感应强度大小随时间变化的关系式为B=0.7+0.6t,则导线中的感应电流方向是a→c→b→a(用字母表示),大小是0.1A.
分析 根据法拉第电磁感应定律来确定感应电动势的大小,并由闭合电路欧姆定律与焦耳定律,则可求出感应电流的大小;再由楞次定律来确定的感应电流的方向.
解答 解:磁感应强度随时间变化的关系式为:Bt=0.7+0.6t(T)
可得:$\frac{△B}{△t}$=0.6
根据法拉第电磁感应定律有:E=$\frac{△B•S}{△t}$=0.6×$\frac{π{r}^{2}}{4}$(S为有效面积,即$\frac{1}{4}$圆面积)
I=$\frac{E}{R}$=0.6×$\frac{π×{1}^{2}}{4×2π×1×\frac{3}{4}}$A=0.1A
根据楞次定律可知,感应电流的方向为a→c→b→a.
故答案为:a→c→b→a,0.1.
点评 考查法拉第电磁感应定律、闭合电路欧姆定律、焦耳定律与楞次定律等规律的应用与掌握,注意磁通量的变化的有效面积与线圈的电阻.

练习册系列答案
相关题目
10.一质点开始时做匀速直线运动,从某时刻起受到一恒力作用.此后,该质点的速度大小不可能的是( )
| A. | 一直增大 | |
| B. | 先逐渐减小至零,再逐渐增大 | |
| C. | 先逐渐增大至某一最大值,再逐渐减小 | |
| D. | 先逐渐减小至某一非零的最小值,再逐渐增大 |
8.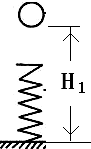 如图所示,一根轻质弹簧竖直固定于水平地面,一质量为m的小球自弹簧正上方离地面的高度为H1处自由落下并压缩弹簧,设速度达到最大时的位置离地面高度为h1最大速度v1;若让此小球从离地面高H2(H2>H1)处自由下落,速度达到最大时位置离地面高度为h2,最大速度为v2,不计空气阻力,则( )
如图所示,一根轻质弹簧竖直固定于水平地面,一质量为m的小球自弹簧正上方离地面的高度为H1处自由落下并压缩弹簧,设速度达到最大时的位置离地面高度为h1最大速度v1;若让此小球从离地面高H2(H2>H1)处自由下落,速度达到最大时位置离地面高度为h2,最大速度为v2,不计空气阻力,则( )
 如图所示,一根轻质弹簧竖直固定于水平地面,一质量为m的小球自弹簧正上方离地面的高度为H1处自由落下并压缩弹簧,设速度达到最大时的位置离地面高度为h1最大速度v1;若让此小球从离地面高H2(H2>H1)处自由下落,速度达到最大时位置离地面高度为h2,最大速度为v2,不计空气阻力,则( )
如图所示,一根轻质弹簧竖直固定于水平地面,一质量为m的小球自弹簧正上方离地面的高度为H1处自由落下并压缩弹簧,设速度达到最大时的位置离地面高度为h1最大速度v1;若让此小球从离地面高H2(H2>H1)处自由下落,速度达到最大时位置离地面高度为h2,最大速度为v2,不计空气阻力,则( )| A. | v1<v2,h1=h2 | B. | v1<v2,h1<h2 | C. | v1=v2,h1<h2 | D. | v1<v2,h1>h2 |
15.下面反映理想气体一定作等容变化规律的图象是( )
| A. |  | B. |  | C. |  | D. |  |
3. 如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )
如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )
 如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )
如图是“嫦娥一号奔月”示意图,卫星发射后通过自带的小型火箭多次变轨,进入地月转移轨道,最终被月球引力捕获,成为绕月卫星,并开展对月球的探测,下列说法正确的是( )| A. | 发射“嫦娥一号”的速度必须达到第二宇宙速度 | |
| B. | 在绕月圆轨道上,卫星周期与卫星质量有关 | |
| C. | 卫星受月球的引力与它到月球中心距离的平方成反比 | |
| D. | 在绕月圆轨道上,卫星受地球的引力大于受月球的引力 |
8. 如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.若在小球A抛出的同时,小球B从同一点Q处开始自由下落,下落至P点的时间为t2,不计空气阻力,则A、B两球在空中运动的时间之比t1:t2等于( )
如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.若在小球A抛出的同时,小球B从同一点Q处开始自由下落,下落至P点的时间为t2,不计空气阻力,则A、B两球在空中运动的时间之比t1:t2等于( )
 如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.若在小球A抛出的同时,小球B从同一点Q处开始自由下落,下落至P点的时间为t2,不计空气阻力,则A、B两球在空中运动的时间之比t1:t2等于( )
如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度v0水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为t1.若在小球A抛出的同时,小球B从同一点Q处开始自由下落,下落至P点的时间为t2,不计空气阻力,则A、B两球在空中运动的时间之比t1:t2等于( )| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:3 |


 在“探究共点力合成规律”的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳,图乙是在白纸上根据实验结果画出的图
在“探究共点力合成规律”的实验中,某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳,图乙是在白纸上根据实验结果画出的图