题目内容
如图甲所示,MN左侧有一垂直纸面向里的匀强磁场.现将一边长为l、质量为m、电阻为R的正方形金属线框置于该磁场中,使线框平面与磁场方向垂直,且bc边与磁场边界MN重合.当t=0时,对线框施加一水平拉力F,使线框由静止开始向右做匀加速直线运动;当t=t时,线框的ad边与磁场边界MN重合.图乙为拉力F随时间t变化的图线.由以上条件可知,磁场的磁感应强度B的大小及t时刻线框的速率v为( )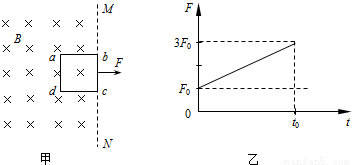
A.
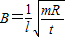
B.
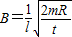
C.
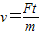
D.
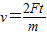
【答案】分析:t=0时刻,感应电流为零,线框受到的安培力为零.由牛顿第二定律可求出加速度,并求出t时刻线框的速率v.当t=t时,由图读出拉力,根据牛顿第二定律列出表达式,结合斜率求出B.
解答:解:t=0时刻,感应电动势E=0,感应电流I=0,安培力F安=BIl=0,
由牛顿第二定律得,F=ma,a=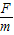 ,v=at=
,v=at=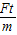
根据牛顿第二定律得,F-F安=ma,又F安=BIl,I=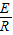 ,E=Blv,
,E=Blv,
得到 F=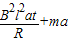
t=t时该,由图读出图线的斜率K=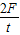 =
=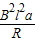 =
=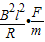
解得B=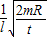
故BC
点评:本题的关键求出安培力,列出牛顿第二定律关于B的表达式,考查读图的能力.这里,安培力是联系力学与电磁感应的桥梁.
解答:解:t=0时刻,感应电动势E=0,感应电流I=0,安培力F安=BIl=0,
由牛顿第二定律得,F=ma,a=
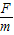 ,v=at=
,v=at=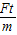
根据牛顿第二定律得,F-F安=ma,又F安=BIl,I=
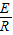 ,E=Blv,
,E=Blv,得到 F=
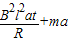
t=t时该,由图读出图线的斜率K=
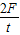 =
=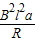 =
=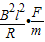
解得B=
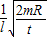
故BC
点评:本题的关键求出安培力,列出牛顿第二定律关于B的表达式,考查读图的能力.这里,安培力是联系力学与电磁感应的桥梁.

练习册系列答案
相关题目
 (2011?朝阳区一模)如图甲所示,MN左侧有一垂直纸面向里的匀强磁场.现将一边长为l、质量为m、电阻为R的正方形金属线框置于该磁场中,使线框平面与磁场垂直,且bc边与磁场边界MN重合.当t=0时,对线框施加一水平拉力F,使线框由静止开始向右做匀加速直线运动;当t=t0时,线框的ad边与磁场边界MN重合.图乙为拉力F随时间变化的图线,不及摩擦阻力.由以上条件可知,磁场的磁感应强度B的大小为( )
(2011?朝阳区一模)如图甲所示,MN左侧有一垂直纸面向里的匀强磁场.现将一边长为l、质量为m、电阻为R的正方形金属线框置于该磁场中,使线框平面与磁场垂直,且bc边与磁场边界MN重合.当t=0时,对线框施加一水平拉力F,使线框由静止开始向右做匀加速直线运动;当t=t0时,线框的ad边与磁场边界MN重合.图乙为拉力F随时间变化的图线,不及摩擦阻力.由以上条件可知,磁场的磁感应强度B的大小为( ) (2011?淮安模拟)如图甲所示,MN左侧有一垂直纸面向里的匀强磁场.现将一边长为l、质量为m、电阻为R的正方形金属线框置于该磁场中,使线框平面与磁场方向垂直,且bc边与磁场边界MN重合.当t=0时,对线框施加一水平拉力F,使线框由静止开始向右做匀加速直线运动;当t=t0时,线框的ad边与磁场边界MN重合.图乙为拉力F随时间t变化的图线.由以上条件可知,磁场的磁感应强度B的大小及t0时刻线框的速率v为( )
(2011?淮安模拟)如图甲所示,MN左侧有一垂直纸面向里的匀强磁场.现将一边长为l、质量为m、电阻为R的正方形金属线框置于该磁场中,使线框平面与磁场方向垂直,且bc边与磁场边界MN重合.当t=0时,对线框施加一水平拉力F,使线框由静止开始向右做匀加速直线运动;当t=t0时,线框的ad边与磁场边界MN重合.图乙为拉力F随时间t变化的图线.由以上条件可知,磁场的磁感应强度B的大小及t0时刻线框的速率v为( )
 电流方向abcda B.
电流方向abcda B.  电流方向adcba
电流方向adcba 电流方向abcda D.
电流方向abcda D.  电流方向abcda
电流方向abcda A.
A. B.
B.
 D.
D.