一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
(1)利用散点图或相关系数r的大小判断变量y对x是否线性相关?为什么?
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(最后结果精确到0.001.参考数据: ,16×11+14×9+12×8+8×5=438,162+142+122+82=660,112+92+82+52=291).
,16×11+14×9+12×8+8×5=438,162+142+122+82=660,112+92+82+52=291).
0 77513 77521 77527 77531 77537 77539 77543 77549 77551 77557 77563 77567 77569 77573 77579 77581 77587 77591 77593 77597 77599 77603 77605 77607 77608 77609 77611 77612 77613 77615 77617 77621 77623 77627 77629 77633 77639 77641 77647 77651 77653 77657 77663 77669 77671 77677 77681 77683 77689 77693 77699 77707 266669
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(最后结果精确到0.001.参考数据:
 ,16×11+14×9+12×8+8×5=438,162+142+122+82=660,112+92+82+52=291).
,16×11+14×9+12×8+8×5=438,162+142+122+82=660,112+92+82+52=291).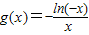 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R.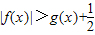 .
. |+|a|=0有实根,求a的取值.
|+|a|=0有实根,求a的取值.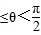 ),求曲线C1、C2交点的极坐标.
),求曲线C1、C2交点的极坐标. 的定义域为( )
的定义域为( )