某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到数据如下表：
（Ⅰ）根据上表可得回归方程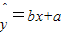
中的b=-20，据此模型预报单价为10元时的销量为多少件？
（Ⅱ）预计在今后的销售中，销量与单价仍然服从（Ⅰ）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）
| 单价x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |
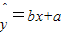中的b=-20，据此模型预报单价为10元时的销量为多少件？（Ⅱ）预计在今后的销售中，销量与单价仍然服从（Ⅰ）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）
某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：
A配方的频数分布表
B配方的频数分布表
（Ⅰ）分别估计用A配方，B配方生产的产品的优质品率；
（Ⅱ）已知用B配方生成的一件产品的利润y（单位：元）与其质量指标值t的关系式为y=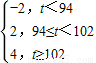
从用B配方生产的产品中任取一件，其利润记为X（单位：元），求X的分布列及数学期望．（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）
0 75039 75047 75053 75057 75063 75065 75069 75075 75077 75083 75089 75093 75095 75099 75105 75107 75113 75117 75119 75123 75125 75129 75131 75133 75134 75135 75137 75138 75139 75141 75143 75147 75149 75153 75155 75159 75165 75167 75173 75177 75179 75183 75189 75195 75197 75203 75207 75209 75215 75219 75225 75233 266669
A配方的频数分布表
| 指标值分组 | [90，94） | [94，98） | [98，102） | [102，106） | [106，110] |
| 频数 | 8 | 20 | 42 | 22 | 8 |
| 指标值分组 | [90，94） | [94，98） | [98，102） | [102，106） | [106，110] |
| 频数 | 4 | 12 | 42 | 32 | 10 |
（Ⅱ）已知用B配方生成的一件产品的利润y（单位：元）与其质量指标值t的关系式为y=
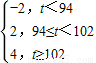
从用B配方生产的产品中任取一件，其利润记为X（单位：元），求X的分布列及数学期望．（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）
）
，
，
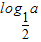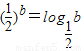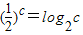，则（ ）