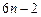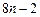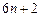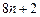已知直线l、m,平面α、β,且l⊥m,m∈β,给出下列四个命题:
①若α∥β,则l⊥m;②若l⊥m,则a∥β;
③若α⊥β,则l⊥m;④若l∥m,则α⊥β.
其中正确命题的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
凸n边形有f(n)条对角线,则凸n+1边形有f(n+1)条对角线数为( )
| A.f(n)+n-1 | B.f(n)+n |
| C.f(n)+n+1 | D.f(n)+n-2 |
在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,……这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形(如下图所示)则第n个三角形数为( )
| A.n | B.n(n+1) |
| C.n2-1 | D.n(n-1) |
用反证法证明命题:“三角形的内角中至少有一个不大于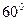 ”时,反设正确的是
”时,反设正确的是
A.设三内角都不大于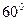 | B.设三内角都大于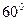 |
C.设三内角至多有一个大于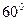 | D.设三内角至多有两个大于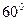 |
下面三段话可组成 “三段论”,则“小前提”是( )
)
①因为指数函数y =" a" x(a > 1 )是增函数;②所以y =" 2" x是增函数;
③而y =" 2" x是指数函数。
| A.① | B.② | C.①② | D.③ |
下面三段话可组成 “三段论”,则“小前提”是( )
①因为指数函数y =" a" x(a > 1 )是增函数;②所以y =" 2" x是增函数;
③而y =" 2" x是指数函数。
| A.① | B.② | C.①② | D.③ |
 块区域,可数得
块区域,可数得 ,则
,则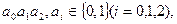 传输信息为
传输信息为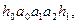 其中
其中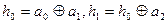 ,
,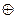 运算规则为
运算规则为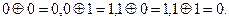 例如原信息为
例如原信息为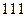 ,则传输信息为
,则传输信息为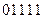 ,传输信息在传输过程中受到干扰可能导致接受信息出错,则下列接受信息一定有误的是
,传输信息在传输过程中受到干扰可能导致接受信息出错,则下列接受信息一定有误的是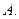
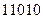
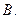
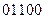
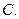
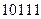
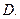
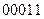


 用火柴棒摆“金鱼”,如图所示:
用火柴棒摆“金鱼”,如图所示: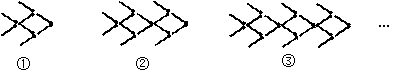
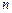 个“金鱼”图需要火柴棒的根数为
个“金鱼”图需要火柴棒的根数为