下列命题中正确的是 ( )
①“若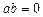 ,则
,则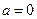 或
或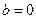 ”
” 的逆命题;
的逆命题;
②“若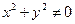 ,则
,则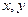 不全为零”的否命题;
不全为零”的否命题;
③“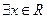 ,使
,使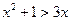 ”的否定;
”的否定;
④“若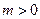 ,则
,则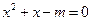 有实根”的逆否命题。
有实根”的逆否命题。
| A.①②③④ | B.①③④ | C.②③④ | D.①②④ |
命题“存在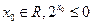 ”的否定是
”的否定是
A.不存在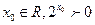 | B.存在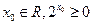 |
C.对任意的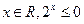 | D.对任意的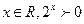 |
“因为四边形ABCD是矩形,所四边形ABCD的对角线相等”,补充以上推理的大前提是  ( )
( )
| A.矩形都是四边形; | B.四边形的对角线都相等; |
| C.矩形都是对角线相等的四边形; | D.对角线都相等的四边形是矩形 |
下面几种推理是类比推理的是( )
A.两条直线平行,同旁内角互补,如果 和 和 是两条平行直线的 是两条平行直线的 同旁内角,则 同旁内角,则  |
| B.由平面向量的运算性质,推测空间向量的运算性质 |
| C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员 |
D.一切偶数都能被2整除, 是偶数,所以 是偶数,所以 能被2整除 能被2整除 |
.观察按下列顺序排列的等式: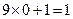 ,
,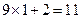 ,
,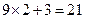 ,
,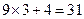 ,
, ,猜想第
,猜想第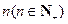 个等式应为 ( )
个等式应为 ( )
A.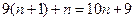 | B.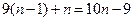 |
C.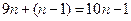 | D.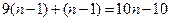 |
有一段演绎推理是这样的:“因为一次函数 =
= +
+ (
( 在R上是增函数,而
在R上是增函数,而 =
= +
+ 是一次函数,所以
是一次函数,所以 =
= +
+ 在R上是增函数” 的结论显然是错误
在R上是增函数” 的结论显然是错误
这是因为 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
下列有关命题的说法正确的是( )
A. ( ( )的图像恒过点(0, )的图像恒过点(0, ) ) |
B.“ ”是 “ ”是 “ ”的必要不充分条件 ”的必要不充分条件 |
C.命题: “ ”的否定是: “ ”的否定是: “ ” ” |
D.“ ”是“ ”是“ 在 在 上为增函数”的充要条件 上为增函数”的充要条件 |
下面是一段演绎推理:
如果直线平行于平面,则这条直线平行于平面内的所有直线;已知直线b//平面 ,直线a
,直线a ;
;
所以直线b//直线a,在这个推理中 ( )
| A.大前提正确,结论错误 | B.小前提与结论都是错误的 |
| C.大、小前提正确,只有结论错误 | D.大前提错误,结论错误 |
下列推理是归纳推理的是
A.已知 为定点,动点 为定点,动点 满足 满足 ,得动点 ,得动点 的轨迹为椭圆 的轨迹为椭圆 |
B.由 求出 求出 ,猜想出数列的前 ,猜想出数列的前  项和 项和 的表达式 的表达式 |
C.由圆 的面积为 的面积为 ,猜想出椭圆 ,猜想出椭圆 的面积为 的面积为 |
| D.科学家利用鱼的沉浮原理制造潜水艇 |
下列表述正确的是( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理。
| A.①②③; | B.②③④; | C.②④⑤; | D.①③⑤。 |