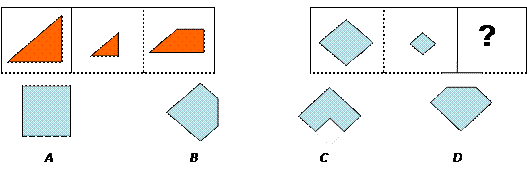
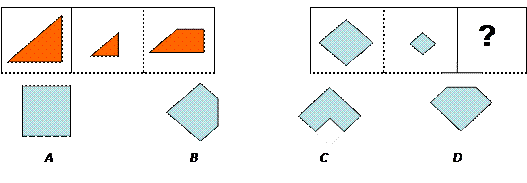
“∵四边形ABCD是矩形,∴四边形ABCD的对角线相等。”补充以上推理的大前提
为( )
| A.正方形都是对角线相等的四边形 | B.矩形都是对角线相等的四边形 |
| C.等腰梯形都是对角线相等的四边形 | D.矩形都是对边相等且平行的四边形 |
有一段演绎推理:“因为对数函数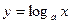 是减函数;已知
是减函数;已知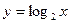 是对数函数,所以
是对数函数,所以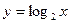 是减函数”,结论显然是错误的,这是因为(***)
是减函数”,结论显然是错误的,这是因为(***)
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
把下面在平面内成立的结论类比地推广到空间,结论还正确的是 ( )
| A.如果一条直线与两条平行线中的一条相交,则它与另一条也相交. |
| B.如果一条直线与两条平行线中的一条垂直,则它与另一条也垂直. |
| C.如果两条直线同时与第三条直线相交,则这两条直线相交. |
| D.如果两条直线同时与第三条直线垂直,则这两条直线平行. |
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间 对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标 变成
变成 ,原来的坐标
,原来的坐标 变成1,等等)。则区间
变成1,等等)。则区间 上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与1重合的点所对应的坐标是
上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与1重合的点所对应的坐标是 ,那么在第
,那么在第 次操作完成后
次操作完成后 ,恰好被拉到与1重合的点对应的坐标是( )
,恰好被拉到与1重合的点对应的坐标是( )
A. 为 为 中所有奇数) 中所有奇数) | B. |
C. 为 为 中所有奇数) 中所有奇数) | D. |
若 表示
表示 的各位数字之和,如
的各位数字之和,如 ,
,
记 ,则
,则 的值是( )
的值是( )
| A.3 | B.5 | C.8 | D.11 |
推理 “1矩形是平行四边形;2正方形是矩形;3所以正方形是平行四边形”中的小前提是( )
| A.1 | B.2 | C.3 | D.1和2 |
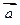 的性质
的性质 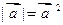 ,可以类比得到复数
,可以类比得到复数 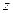 的性质
的性质 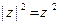 ;
;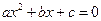 (a 、b 、c ∈ R )有两个不同实根的条件是
(a 、b 、c ∈ R )有两个不同实根的条件是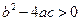 ,类比可以得到 方程
,类比可以得到 方程 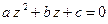 (a 、b 、c ∈ C)有两个不同复数根的条件是
(a 、b 、c ∈ C)有两个不同复数根的条件是 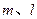 ,平面
,平面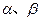 ,且
,且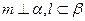 ,给出下列命题:①若
,给出下列命题:①若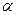 ∥
∥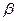 ,则m⊥
,则m⊥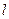 ;
;