因为对数函数y=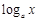 是减函数(大前提),而y=
是减函数(大前提),而y=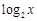 是对数函数(小前提),所以y=
是对数函数(小前提),所以y=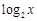 是减函数(结论)”。上面推理是( )
是减函数(结论)”。上面推理是( )
| A.大前提错,导致结论错。 | B.小前提错,导致结论错 |
| C.推理形式错,导致结论错。 | D.大前提和小前提都错,导致结论错。 |
如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…)则在第n个图形中共有( )个顶点. ( )
| A.(n+1)(n+2) | B.(n+2)(n+3) | C. | D.n |
用反证法证明“a、b∈N+,ab可被5整除,那么,a、b中至少有一个能被5整除”时,假设的内容是
| A.a不能被5 整除 | B.a,b不能被5整除 |
| C.a、b都不能被5 整除 | D.以上都不对 |
下面几种推理是类比推理的是 ( )
A.两条直线平行,同旁内角互补,如果 和 和 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则  |
| B.由平面向量的运算性质,推测空间向量的运算性质 |
| C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员,; |
D.一切偶数都能被2整除, 是偶数,所以 是偶数,所以 能被2整除 能被2整除 |
三角形的面积为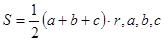 为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
A.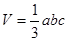 |
B.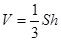 |
C.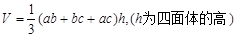 |
D.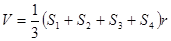 ( (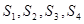 分别为四面体的四个面的面积,r为四面体内切球的半径) 分别为四面体的四个面的面积,r为四面体内切球的半径) |
下列表述正确的是( )
①归纳推理是由部分到整体的推理;
②归纳推理是由一般到一般的推理;
③演绎推理是由一般到特殊的推理;
④类比推理是由特殊到一般的推理;
⑤类比推理是由特殊到特殊的推理。
| A.①②③; | B.②③④; | C.②④⑤; | D.①③⑤。 |
由数列1,10,100,1000,……猜测该数列的第n项可能是( )。
| A.10n; | B.10n 1; | C.10n+1; | D.11n. |
将正偶数按下表排列则2012所在的位置是
| | 第1列 | 第2列 | 第3列 | 第4列 | 第5列 |
| 第一行 | | 2 | 4 | 6 | 8 |
| 第二行 | 16 | 14 | 12 | 10 | |
| 第三行 | | 18 | 20 | 22 | 24 |
| 第四行 | 32 | 30 | 28 | 26 | |
| …… | | …… | | …… | |
B.第252行第4列
C.第251行第3列
D.第251行第4列
根据右边给出的数塔猜测123456 9+8=( )
9+8=( ) 
| A.1111110 |
| B.1111111 |
| C.1111112 |
| D.1111113 |
有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 ∥平面
∥平面 ,则直线
,则直线 ∥直线
∥直线 ”的结论显然是错误的,这是因为( )
”的结论显然是错误的,这是因为( )
| A.大前提错误 | B.小前提错误 |
| C.推理形式错误 | D.非以上错误 |