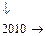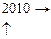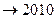对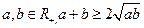 ------------- 大前提
------------- 大前提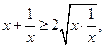 -------------- 小前提
-------------- 小前提
所以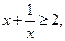 --
-- -------
------- ------- 结论
------- 结论
以上推理 过程中的错误为
过程中的错误为 ( )
( )
| A.大前提 | B.小前提 | C.结论 | D.无错误 |
由“在平面内三角形的内切圆的圆心到三边的距离相等”联想到“在空间中内切于三棱锥的球的球心到三棱锥四个面的距离相等”这一推理过程是 ( )
| A.归纳推理 | B.类比推理 | C.演绎推理 | D.联想推理 |
已知x>0,由不等式 可以推广为( )
可以推广为( )
A. | B. |
C. | D. |
.古希腊著名的毕达哥拉斯学 派把1.3.610……这样的数称为“三角形数
派把1.3.610……这样的数称为“三角形数 ”,而把1.4.9.16……这样的数称为“正方形数”。如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为 ( )
”,而把1.4.9.16……这样的数称为“正方形数”。如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为 ( )
①13=3+10; ②25=9+16; ③36=15+21; ④ 49=18+31; ⑤6
49=18+31; ⑤6 4=28+36
4=28+36
| A.③⑤ | B.②④⑤ | C.②③④ | D.①②③⑤ |
已知△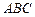 中,
中,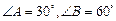 ,求证
,求证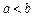 .
.
证明: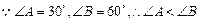 ,
,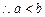 ,画线部分是演绎推理的是()
,画线部分是演绎推理的是()
| A.大前提 | B.小前提 | C.结论 | D.三段论 |
有下列四个命题,其中真命题有:
①“若 ,则
,则 、
、 互为相反数”的逆命题
互为相反数”的逆命题
②“ 全等三角形的面积相等”的否命题
全等三角形的面积相等”的否命题
③“若 ,则
,则 有实根”的逆命题
有实根”的逆命题
④“不等边 三角形的三个内角相等”的逆否命题
三角形的三个内角相等”的逆否命题
其中真 命题的序号为:
命题的序号为:
| A.①② | B.② ③ ③ | C.①③ | D.③④ |
下面推 理是类比推理的是( )
理是类比推理的是( )
| A.两条直线平行,则同旁内角互补,若∠A和∠B是同旁内角,则∠A+∠B=180° |
| B.由平面三角形的性质,推测空间四边形的性质 |
| C.某校高二有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此推测各班都超过50位团员 |
D.一 切偶数能被2整除,2100是偶数,故2100能被2整数 切偶数能被2整除,2100是偶数,故2100能被2整数 |
下面几种推理是类比推理的是( )
A.两条直线平行,同旁内角互补,如果∠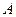 和∠ 和∠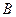 是两条平行直线的同旁内角,则∠ 是两条平行直线的同旁内角,则∠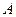 +∠ +∠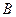 =1800 =1800 |
| B.由平面三角形的性质,推测空间四边形的性质 |
| C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员. |
D.一切偶数都能被2整除,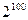 是偶数,所以 是偶数,所以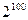 能被2整除. 能被2整除. |
 9+8=( )
9+8=( ) 
 5
5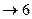
 9
9
 7
7
 11
11