(本小题满分12分)
某电视台为了宣传某沿江城市经济崛起的情况,特举办了一期有奖知识问答活动,活动对18—48岁的人群随机抽取 n人回答问题“沿江城市带包括哪几个城市”,统计数据结果如下表:
| 组数 | 分组 | 回答正 确的人数 | 占本组 的频率 |
| 第1组 | [18,28〕 | 240 | X |
| 第2组 | [28,38〕 | 300 | 0.6 |
| 第3组 | [38,48〕 | a | 0.4 |

(Ⅰ)分别求出n,a,x的值;
(Ⅱ)若以表中的频率近似看作各年龄组正确回答问题的概率,规定年龄在[38,48〕内回答正确的得奖金200元,年龄在[18,28〕内回答正确的得奖金100元。主持人随机请一家庭的两个成员(父亲46岁,孩子21岁)回答正确,求该家庭获得奖金
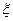 的分布列及数学期望(两人回答问题正确与否相互独立)。
的分布列及数学期望(两人回答问题正确与否相互独立)。 (本小题满分12分)
在一次“研究性学习”中,三班第一组的学生对人们的休闲方式的进行了一次随机调查,
| 性别 休闲方式 | 看电视 | 运动 |
| 女 | 15 | 10 |
| 男 | 5 | 20 |
试判断性别与休闲方式是否有关系?作为这个判断出错的可能性有多大?
(本小题满分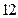 分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ) 测得该年级所抽查的100名同学身高(单位:厘米) 频率分布直方图如右图:
(ⅰ) 统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望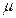 及标准差
及标准差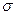 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在 范围中的学生的人数.
范围中的学生的人数.
(Ⅲ) 如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| | 身高达标 | 身高不达标 | 总计 |
| 积极参加体育锻炼 | 40 | | |
| 不积极参加体育锻炼 | | 15 | |
| 总计 | | | 100 |
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K
 =
=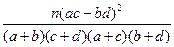 ,参考数据:
,参考数据:P(K  k) k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
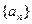 的
的 前六项。
前六项。 学生,试估计该校新生的近视率
学生,试估计该校新生的近视率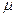 的大
的大
 么?
么?
 ,求
,求 .
. 的身高,单位:cm),分组情况如下:
的身高,单位:cm),分组情况如下:

 65.5
65.5


 ,
, 的值,并画出频率分布直方图;
的值,并画出频率分布直方图; 满分12分)
满分12分)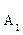 ,
,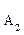 ,…
,…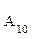 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:
 ,也可能亏损
,也可能亏损 ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为 和
和 ;
; ,可能亏损
,可能亏损 ,也可能不赔不赚,且这三种情况发生的概率分别为
,也可能不赔不赚,且这三种情况发生的概率分别为 、
、 和
和

 ,
, )
) 人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在
人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在 ).
).
 的频率;
的频率; 人作进一步分析,则月收入在
人作进一步分析,则月收入在 的这段应
的这段应 出多少人?
出多少人?