设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线的方程为( )
| A.y2=±4x | B.y2=±8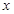 | C.y2=4x | D.y2=8x |
如图,已知点B是椭圆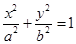
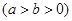 的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴,
的短轴位于x轴下方的端点,过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴,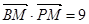 ,若点P的坐标为(0,t),则t的取值范围是( )
,若点P的坐标为(0,t),则t的取值范围是( )
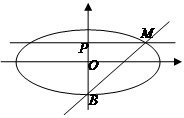 |
A.0<t<3 B.0<t≤3 C.
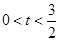 D.
D.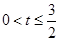
如图,已知点B是椭圆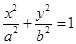
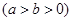 的短轴位于x轴下方的端点,
的短轴位于x轴下方的端点,
过B作斜率为1的直线交椭圆于点M,点P在y轴上,且PM//x轴,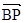 ?
? 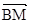 =9,若点P的坐标为(0,t),则t的取值范围是 ( )
=9,若点P的坐标为(0,t),则t的取值范围是 ( )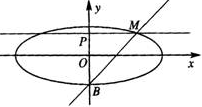
| A.0<t<3 | B.0<t≤3 | C.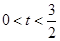 | D.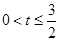 |
若抛物线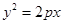 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则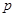 的值为( )
的值为( )
| A.-6 | B.6 | C.-4 | D.4 |
若抛物线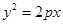 的焦点与双曲线
的焦点与双曲线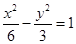 的右焦点重合,则
的右焦点重合,则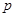 的值为( )
的值为( )
| A.-6 | B.6 | C.-4 | D.4 |
设F1,F2是椭圆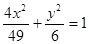 的两个焦点,P是椭圆上的点,且
的两个焦点,P是椭圆上的点,且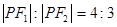 ,
,
则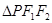 的面积为( )
的面积为( )
| A.4 | B.6 | C.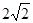 | D.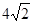 |
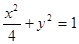 的右焦点,椭圆上的点与点F的最大距离为M,最小距离为N,则椭圆上与点F的距离等于
的右焦点,椭圆上的点与点F的最大距离为M,最小距离为N,则椭圆上与点F的距离等于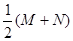 的点的坐标是
的点的坐标是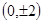
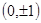
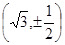
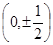
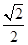 的直线
的直线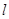 与椭圆
与椭圆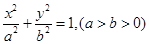 交于不同的两点,且这两个交点在
交于不同的两点,且这两个交点在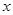 轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )
轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )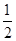
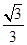
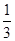
 过抛物线
过抛物线 的焦点
的焦点 ,交抛物线于
,交抛物线于 两点,且点
两点,且点 在
在 轴上方,
轴上方, ,则
,则 的取值范围是( )
的取值范围是( )


