要证明可选择的方法有以下几种，其中最合理的是  （   ）

A．综合法

B．分析法

C．归纳法

D．类比法

已知，由不等式……
可以推出结论=                                

A．

B．

C．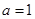

D．

对任意正数，不等式恒成立，则实数的取值范围是（ ）

A．

B．

C．

D．

若0＜x₁＜x₂,  0＜y₁＜y₂，且x₁＋x₂=y₁＋y₂=1，则下列代数式中值最大的是（   ）

A．x1y1＋x2y2

B．x1x2＋y1y2

C．x1y2＋x2y1

D．

已知a,b,c是正实数,且a+b+c=1,则的最小值为(     )

用反证法证明命题“三角形的三个内角中至多有一个是钝角”时， 假设正确的是（    ）

二维形式的柯西不等式可用（   ）表示

A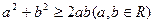．	B．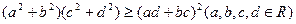
C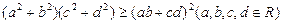．	D．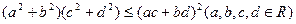

若不等式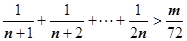对于大于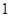的一切正整数都成立，则正整数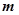
的最大值为  （ ）

用反证法证明：“”，应假设为：

A．

B．

C．

D．

由，猜想若，，则与之间大
小关系为（　）
A．相等      B．前者大      C．后者大       D．不确定