在 上定义运算:
上定义运算: 若不等式
若不等式 对一切实数
对一切实数 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
a,b是正实数,则 的最小值是( )
的最小值是( )
| A.8 | B.4 | C.32 | D.16 |
若0<a<1,则不等式(x-a)(x-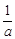 )>0的解集是
)>0的解集是
A.(a,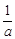 ) ) | B.(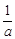 ,a) ,a) |
C.(-∞,a)∪(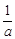 ,+∞) ,+∞) | D.(-∞,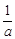 )∪(a,+∞) )∪(a,+∞) |
若a>b, ,则下列命题中成立的是
,则下列命题中成立的是
A. | B. | C. | D. |
当x>1时,不等式x+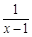 ≥a恒成立,则实数a的取值范围是( )
≥a恒成立,则实数a的取值范围是( )
| A.(-∞,2] | B.[2,+∞) | C.(-∞,3] | D.[3,+∞) |
若a>0,b>0,a+b=2,则下列不等式对一切满足条件的a,b恒成立的是( )
①ab≤1; ② +
+ ≤
≤ ; ③a2+b2≥2; ④
; ③a2+b2≥2; ④ ≥2
≥2
| A.①②③④ | B.①③④ | C.③④ | D.②③④ |
某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与仓库到车站的距离成正比,如果在距离车站10 km处建仓库,这两项费用y1和y2分别为2万元和8万元,那么,要使这两项费用之和最小,仓库应建在离车站( )
| A.5km处 | B.4km处 | C.3km处 | D.2km处 |
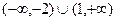 C.(-2,1) D.(-1,2)
C.(-2,1) D.(-1,2)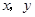 满足约束条件
满足约束条件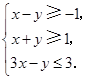 则①函数
则①函数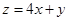 的最大值为11 ;②函数z="(x" —1) 2 + (y+1)2的最小值是1 ;③函数
的最大值为11 ;②函数z="(x" —1) 2 + (y+1)2的最小值是1 ;③函数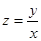 的最小值为0 ;以上正确的序号有( )
的最小值为0 ;以上正确的序号有( )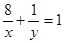 ,则
,则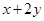 的最小值是
的最小值是