如果有穷数列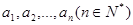 满足条件:
满足条件: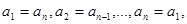
即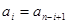 ,
,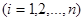 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列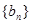 是项数不超过
是项数不超过 的“对称数列”,并使得
的“对称数列”,并使得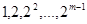 依次为该数列中连续的前
依次为该数列中连续的前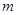 项,则数列
项,则数列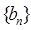 的前2009项和
的前2009项和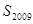 所有可能的取值的序号为 ( )
所有可能的取值的序号为 ( )
① ②
② ③
③ ④
④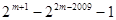
| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
已知正项等差数列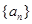 的前20项的和为100,那么
的前20项的和为100,那么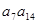 的最大值为
的最大值为
| A.75 | B.100 | C.50 | D.25 |
已知数列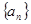 的前n项和为
的前n项和为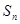 ,且
,且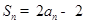 , 则
, 则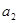 等于
等于
| A.4 | B.2 | C.1 | D.-2 |
已知 求数列满足
求数列满足 ,
, ,则
,则 是递增数列,则实数
是递增数列,则实数 取值范围是( )
取值范围是( )
A. | B. | C. | D. |
已知正项数列 为等比数列,且
为等比数列,且 是
是 与
与 的等差中项,若
的等差中项,若 ,则该数列的前5项的和为 ( )
,则该数列的前5项的和为 ( )
A. | B. | C. | D.以上都不正确 |
已知数列 中,
中, ,则这个数列的前
,则这个数列的前 项和
项和 等于 ( )
等于 ( )
A. | B. | C. | D. |
已知a,b∈(0,+∞),A为a,b的等差中项,正数G为a,b的等比中项,则ab与AG的大小关系是( )
| A.ab=AG | B.ab≥AG | C.ab≤AG | D.不能确定 |
已知数列 的通项公式是
的通项公式是 ,那么这个数列是
,那么这个数列是
| A.递增数列 | B.递减数列 | C.常数列 | D.摆动数列 |
已知数列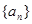 的通项公式是
的通项公式是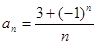 :,则
:,则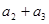 的值为
的值为
| A. 2 | B.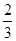 | C.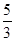 | D.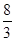 |
