在数列 中,若对任意
中,若对任意 的都有
的都有 (
( 为常数),则
为常数),则 称为“等差比数列”。下面是对“等差比数列”的判断:①
称为“等差比数列”。下面是对“等差比数列”的判断:① 不可能为
不可能为 ;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④等差比数列中可以有无数项为
;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④等差比数列中可以有无数项为 。其中正确的有( )
。其中正确的有( )
| A.①② | B.①②③ | C.①④ | D.①②③④ |
已知a1=3,a2=6且an+2=an+1-an则a33为( )
| A.3 | B.-3 | C.6 | D.-6 |
若f(n)=1+2+3+…+(n-1)+n+(n-1)+…+3+2+1,则f(2)=
| A.1 | B.2 | C.3 | D.4 |
数列 满足
满足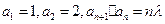 (
(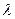 为常数,
为常数,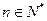 ),则
),则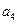 等于( )
等于( )
| A.1 | B.2 | C.3 | D.4 |
如图,坐标纸上的每个单元格的边长为1,
由下往上的六个点:l,2,3,4,5,6的
横、纵坐标分别对应数列
的前l2项(即横坐标为奇数项,纵坐标为
偶数项),按如此规律下去,
则 等于 ( )
等于 ( )
| A.1003 | B.1005 |
| C.1006 | D.2011 |

若数列 满足
满足 (
( 为正常数,
为正常数, ),则称
),则称 为“等方差数列”.
为“等方差数列”.
甲:数列 为等方差数列;乙:数列
为等方差数列;乙:数列 为等差数列,则甲是乙的 ( )
为等差数列,则甲是乙的 ( )
| A.充分不必条件 | B.必不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知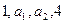 成等差数列,
成等差数列,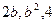 成等比数列,则
成等比数列,则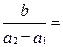 ( )
( )
| A.2 | B.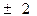 | C.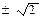  | D.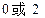 |
 万元,年利率为
万元,年利率为 ,按复利计算,从2010年末开始,每年末偿还一定金额,计划第5年底还清,则每年应偿还的金额数为( )万元.
,按复利计算,从2010年末开始,每年末偿还一定金额,计划第5年底还清,则每年应偿还的金额数为( )万元.




 012箭头的方向是 ( )
012箭头的方向是 ( )




