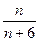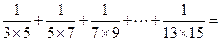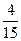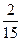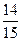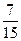已知等比数列 的各项为均不等于1的正数,数列
的各项为均不等于1的正数,数列 满足
满足 则数列
则数列 的前n项和的最大值等于 ( )
的前n项和的最大值等于 ( )
| A.126 | B.130 | C.132 | D.134 |
数列 的前n项和
的前n项和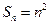 ,则
,则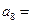 ( )
( )
| A.15 | B.16 | C.49 | D.64 |
设数列 的通项公式
的通项公式 ,若使得
,若使得 取得最小值,n=" " ( )
取得最小值,n=" " ( )
| A. 8 | B.8、9 |
| C. 9 | D.9、10 |
数列 的通项公式是
的通项公式是 ,若前n项和为
,若前n项和为 则n等于( )
则n等于( )
| A.12 | B.11 | C.10 | D.9 |
数列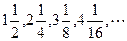 前n项的和为( )
前n项的和为( )
A.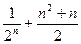 | B.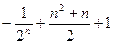 |
C.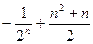 | D.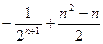 |
数列1、1+2、1+2+22、…、1+2+22+…+2n-1…的前n项和为 ( )
| A.2n—n—1 | B.2n+1—n—2 | C.2n | D.2n+1—n |
定义:若数列 对任意的正整数n,都有
对任意的正整数n,都有 (d为常数),则称
(d为常数),则称 为“绝对和数列”,d叫做“绝对公和”,已知“绝对和数列”
为“绝对和数列”,d叫做“绝对公和”,已知“绝对和数列” ,“绝对公和”
,“绝对公和” ,则其前2010项和
,则其前2010项和 的最小值为 ( )
的最小值为 ( )
| A.—2006 | B.—2009 | C.—2010 | D.—2011 |
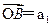
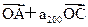 ,且A、B、C三点共线(该直线不过原点O),则S200=( )
,且A、B、C三点共线(该直线不过原点O),则S200=( )
 C.200 D.201
C.200 D.201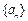 的各项均为正数,
的各项均为正数,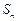 为其前n项和,对于任意的
为其前n项和,对于任意的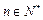 ,总有
,总有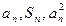 成等差数列,又记
成等差数列,又记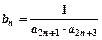 ,数列
,数列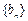 的前n项和Tn=( )
的前n项和Tn=( )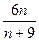 B.
B.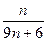 C.
C.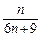 D.
D.