古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如: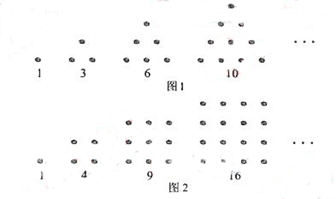
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…这样的数成为正方形数。下列数中既是三角形数又是正方形数的是( )
| A.289 | B.1024 | C.1225 | D.1378 |
数列 的第10项是( )
的第10项是( )
A. | B. | C. | D. |
已知(z-x)2=4(x-y)(y-z),则 ( )
A.x,y,z成等差数列 | B.x,y,z成等比数列 |
C. 成等差数列 成等差数列 | D. 成等比数列 成等比数列 |
设a1,a2,…,a50是从-1,0,1这三个整数中取值的数列,若a1+a2+…+a50=9,
且(a1+1)2+(a2+1)2+…+(a50+1)2=107,则a1,a2,…,a50中有0的个数为( )
| A.10 | B.11 | C.12 | D.13 |
已知{an}是递增的数列,且对于任意n∈N*,都有an=n2+λn成立,则实数λ的取
值范围 ( )
| A.λ>0 | B.λ<0 | C.λ="0" | D.λ>-3 |
若数列{an}前8项的值各异,且an+8=an对任意n∈N*都成立,则下列数列中可取
遍{an}前8项值的数列为 ( )
| A.{a2k+1} | B.{a3k+1} | C.{a4k+1} | D.{a6k+1} |
已知数列{an}中,an=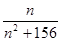 (n∈N),则数列{an}的最大项是( )
(n∈N),则数列{an}的最大项是( )
| A.第12项 | B.第13项 |
| C.第12项或13项 | D.不存在 |
“公差为0的等差数列是等比数列”;“公比为 的等比数列一定是递减数列”;“a,b,c
的等比数列一定是递减数列”;“a,b,c
三数成等比数列的充要条件是b2=ac”;“a,b,c三数成等差数列的充要条件是2b=a+c”,以上
四个命题中,正确的有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设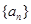 是各项为正数的无穷数列,
是各项为正数的无穷数列,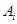 是边长为
是边长为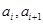 的矩形面积(
的矩形面积(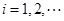 ),则
),则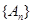 为等比数列的充要条件为( )
为等比数列的充要条件为( )
A.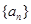 是等比数列。 是等比数列。 |
B.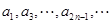 或 或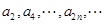 是等比数列。 是等比数列。 |
C.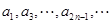 和 和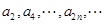 均是等比数列。 均是等比数列。 |
D.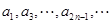 和 和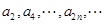 均是等比数列,且公比相同。 均是等比数列,且公比相同。 |
数列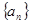 的通项公式
的通项公式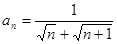 ,则该数列的前( )项之和等于9。
,则该数列的前( )项之和等于9。
( )
| A.98 | B.99 | C.96 | D.97 |