函数 的单调递增区间是
的单调递增区间是
A. | B.(0,2) | C.(1,3) | D. |
观察 ,
, ,
, ,由归纳推理可得:若
,由归纳推理可得:若 是定义在
是定义在 上的奇函数,记
上的奇函数,记 为
为 的导函数,则
的导函数,则
A. | B. | C. | D. |
定积分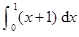 的值为
的值为
A.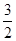 | B.1 | C.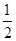 | D.2 |
函数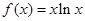 ,则 ( )
,则 ( )
A.在 上递增; 上递增; | B.在 上递减; 上递减; |
C.在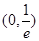 上递增; 上递增; | D.在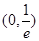 上递减 上递减 |
一个物体的位移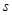 (米)和与时间
(米)和与时间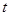 (秒)的关系为
(秒)的关系为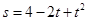 ,则该物体在4秒末的瞬时速度是( )
,则该物体在4秒末的瞬时速度是( )
| A.12米/秒 | B.8米/秒 | C.6米/秒 | D.8米/秒 |
已知函数 ,若有
,若有 ,则b的取值范围为( )
,则b的取值范围为( )
A. | B. |
C. | D. |
设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x·f′(x)的图象的一部分,则f(x)的极大值与极小值分别是
| A.f(1)与f(-1) | B.f(-1)与f(1) | C.f(-2)与f(2) | D.f(2)与f(-2) |

设函数 是可导的函数,若满足
是可导的函数,若满足 ,则必有
,则必有
A. | B. |
C. | D. |
图中由函数 的图象与
的图象与 轴围成的阴影部分面积,用定积分可表示为
轴围成的阴影部分面积,用定积分可表示为
A. | B. |
C. | D. |
已知函数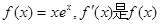 的导函数,则
的导函数,则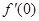 等于
等于
| A.-2 | B.-1 | C.0 | D.1 |