已知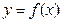 是偶函数,而
是偶函数,而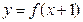 是奇函数,且对任意
是奇函数,且对任意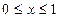 ,都有
,都有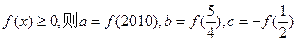 的大小关系是 ( )
的大小关系是 ( )
A.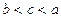 | B.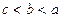 | C.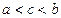 | D.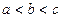 |
如图所示, 是定义在区间
是定义在区间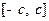 (
(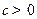 )上的奇函数,令
)上的奇函数,令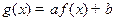 ,并有关于函数
,并有关于函数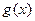 的四个论断:
的四个论断:
①对于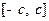 内的任意实数
内的任意实数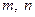 (
(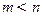 ),
),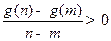 恒成立;
恒成立;
②若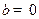 ,则函数
,则函数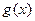 是奇函数;
是奇函数;
③若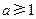 ,
,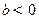 ,则方程
,则方程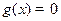 必有3个实数根;
必有3个实数根;
④若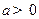 ,则
,则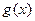 与
与 有相同的单调性.
有相同的单调性.
其中正确的是( )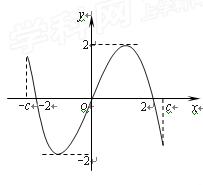
| A.②③ | B.①④ |
| C.①③ | D.②④ |
定义在[0,1]上的函数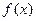 满足
满足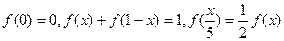 ,且当
,且当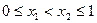 时,
时,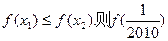 等于 ( )
等于 ( )
A.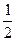 | B.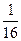 | C.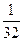 | D.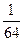 |
设函数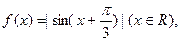 则
则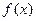 ( )
( )
A.在区间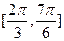 上是增函数 上是增函数 | B.在区间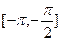 上是减函数 上是减函数 |
C.在区间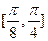 上是增函数 上是增函数 | D.在区间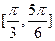 上是减函数 上是减函数 |
已知函数
 ,则
,则 与
与 两函数图象的交点个数为 ( )
两函数图象的交点个数为 ( )
A. | B. | C.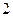 | D.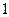 |
设函数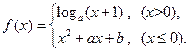 若
若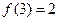 ,
,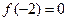 ,则
,则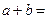
A.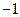 | B. 0 | C.1 | D.2 |
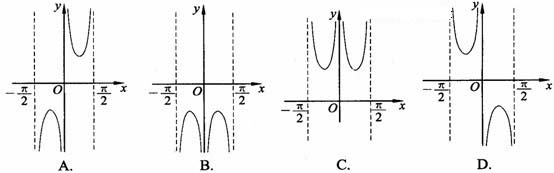
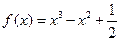 的图象大致是
的图象大致是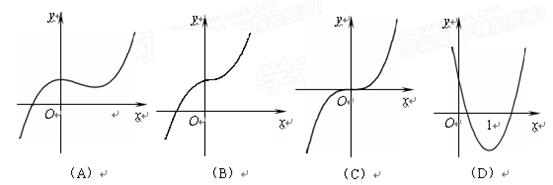
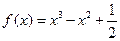 的图象大致是
的图象大致是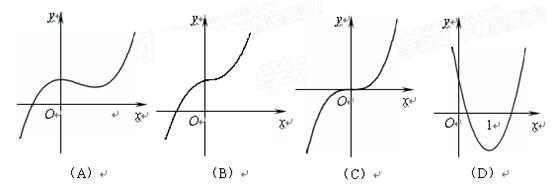
 的一条性质:“存在常数M,使得
的一条性质:“存在常数M,使得 对于定义域中的一切实数
对于定义域中的一切实数 均成立。”则下列函数中具有这条性质的函数是 ( )
均成立。”则下列函数中具有这条性质的函数是 ( )



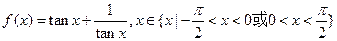 的图像为( )
的图像为( )