某单位为了了解用电量y度与气温![]() 之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
| 气温(0C) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
由表中数据得线性回归方程![]() 中b=-2,预测当气温为
中b=-2,预测当气温为![]() 时,用电量的度数约为▲____ .
时,用电量的度数约为▲____ .
(本小题12分)
为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 是否需要志愿 性别 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由
 附:
附:
(本小题满分12分)某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日 期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差 | 10 | 11 | 13 | 12 | 8 |
| 发芽数 | 23 | 25 | 30 | 26 | 16 |
(Ⅰ)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,求事件“m ,n均不小于25”的概率.
,求事件“m ,n均不小于25”的概率.
(Ⅱ)若选取的是3月1日与3月5日的两组数据,请根据3月2日至3月4日的数据,求出y关于x的线性回归方程![]() ;
;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅱ)中所得的线性回归方程是否可靠?
(参考公式:回归直线的方程是![]() ,其中
,其中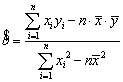 ,
,![]() ,)
,)
. (本小题满分13分)
某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
|
| 2 | 4 | 5 | 6 | 8 |
|
| 30 | 40 | 60 | 50 | 70 |
(Ⅰ)求回归直线方程;
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率。
(参考数据:![]()
![]()
![]() ,
,
参考公式:回归直线方程![]() ,其中
,其中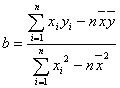 )
)